题目内容
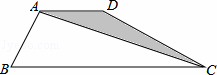
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是( )
|
| A. |
| B. |
| C. | 2 | D. |
|
A
解:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.设AB=AD=x.
又∵AD∥BC,
∴四边 形AEFD是矩形形,
形AEFD是矩形形,
∴AD=EF=x.
在Rt△ABE中,∠ABC=60°,则∠BAE =30°,
=30°,
∴BE= AB=
AB= x,
x,
∴DF=AE= =
= x,
x,
在Rt△CDF中,∠FCD=30°,则CF=DF•cot30°= x.
x.
又BC=6,
∴BE+EF+CF=6,即 x+x+
x+x+ x=6,
x=6,
解得 x=2
∴△ACD的面积是: AD•DF=
AD•DF= x×
x× x=
x= ×22=
×22= ,
,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知⊙O1与⊙O2的半径分别是3cm和5cm,两圆的圆心距为4cm,则两圆的位置关系是( )
|
| A. | 相交 | B. | 内切 | C. | 外离 | D. | 内含 |



 ABC外接圆半径为R,且2R(
ABC外接圆半径为R,且2R( )=
)= ,则角C=( )
,则角C=( )
 的取值范围.
的取值范围.
 .
. ,求DE的长.
,求DE的长.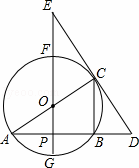
 的图象经过平面直角坐标系的四个象限,那么a的取值范围是
的图象经过平面直角坐标系的四个象限,那么a的取值范围是 