题目内容
16. 如图,某建筑物BC顶部有一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.
如图,某建筑物BC顶部有一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.
分析 根据题意分别在两个直角三角形中求得AF和BF的长后求差即可得到旗杆的高度,进而求得BC的高度.
解答  解:根据题意得DE=1.56,EC=21,∠ACE=90°,∠DEC=90°.
解:根据题意得DE=1.56,EC=21,∠ACE=90°,∠DEC=90°.
过点D作DF⊥AC于点F.
则∠DFC=90°∠ADF=47°,∠BDF=42°.
∵四边形DECF是矩形.
∴DF=EC=21,FC=DE=1.56,
在直角△DFA中,tan∠ADF=$\frac{AF}{DF}$,
∴AF=DF•tan47°≈21×1.07=22.47(m).
在直角△DFB中,tan∠BDF=$\frac{BF}{DF}$,
∴BF=DF•tan42°≈21×0.90=18.90(m),
则AB=AF-BF=22.47-18.90=3.57≈3.6(m).
BC=BF+FC=18.90+1.56=20.46≈20.5(m).
答:旗杆AB的高度约是3.6m,建筑物BC的高度约是20.5米.
点评 此题考查的知识点是解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,先得到等腰直角三角形,再根据三角函数求解.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
6.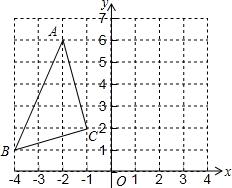 如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为( )
如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为( )
 如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为( )
如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为( )| A. | (4,3) | B. | (2,4) | C. | (3,1) | D. | (2,5) |
 如图,已知AB∥CD,点P在直线CD上,∠APB=100°,∠A=(2x+12)°,∠BPD=(4x+8)°,那么x=10.
如图,已知AB∥CD,点P在直线CD上,∠APB=100°,∠A=(2x+12)°,∠BPD=(4x+8)°,那么x=10. 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,EF=2,那么AH等于6.
如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,EF=2,那么AH等于6. 如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑) 如图,在?ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
如图,在?ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E. 如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4米,AB=6米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4米,AB=6米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)