题目内容
 如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD.
如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD.
(1)求证:AC=BD
(2)若OF⊥CD于F,OG⊥AB于G,问:四边形OFEG是何特殊四边形?并说明理由.
 (1)证明:∵AB=CD,
(1)证明:∵AB=CD,∴
 =
=
∴
 -
- =
= -
- ,即
,即 =
=
∴AC=BD
(2)四边形OFEG是正方形.
理由:连接OA、OD.
∵AB⊥CD,OF⊥CD,OG⊥AB,
∴四边形OFEG是矩形;
∵OF⊥CD,OG⊥AB,
∴DF=
 CD,AG=
CD,AG= AB,
AB,∵AB=CD,∴DF=AG;
∵OD=OA,
∴Rt△OFD≌Rt△OGA (HL)
∴OF=OG,
∴矩形OFEG是正方形.
分析:(1)根据已知条件AB=CD可以推知
 =
= ,然后由图可以知
,然后由图可以知 -
- =
= -
- ,即
,即 =
= ;由圆心角、弧、弦间的关系可以证得AC=BD;
;由圆心角、弧、弦间的关系可以证得AC=BD;(2)连接OA、OD.首先根据矩形的判定定理可以推知四边形OFEG是矩形;然后由已知条件AB=CD、垂径定理推知DF=AG,再由圆的半径OA=OD可以证得Rt△OFD≌Rt△OGA (HL),由全等三角形的对应边相等可以证得OF=OG;最后根据正方形的判定定理可知矩形OFEG是正方形.
点评:本题考查了垂径定理、全等三角形的判定与性质、弧与弦的关系以及正方形的判定.在解答(2)时,利用了“邻边相等的矩形是正方形”.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 13、已知:如图,⊙O的两条弦AE、BC相交于点D,连接AC、BE.若∠ACB=60°,则下列结论中正确的是( )
13、已知:如图,⊙O的两条弦AE、BC相交于点D,连接AC、BE.若∠ACB=60°,则下列结论中正确的是( )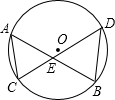 如图,⊙O的两条弦AB、CD相交于点E,连接AC、BD,试证明:AE•BE=CE•DE.
如图,⊙O的两条弦AB、CD相交于点E,连接AC、BD,试证明:AE•BE=CE•DE. 如图,⊙O的两条弦AB、CD相交于E,如果AE=2,EB=6,CE=3,那么CD=
如图,⊙O的两条弦AB、CD相交于E,如果AE=2,EB=6,CE=3,那么CD= 如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则⊙O的半径是
如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则⊙O的半径是 如图,⊙O的两条弦AB、CD互相垂直,垂足为点E,且⊙O的半径为2,AB与CD两弦长的平方和等于28,则OE等于( )
如图,⊙O的两条弦AB、CD互相垂直,垂足为点E,且⊙O的半径为2,AB与CD两弦长的平方和等于28,则OE等于( )