题目内容
20.先确定下列抛物线的开口方向、对称轴和顶点,再描点画图(1)y=-3x2+12x-3 (2)y=4x2-24x+26.
分析 可先把抛物线解析式化为顶点式,容易确定出开口方向、对称轴及顶点坐标,再利用描点法可画出其图象.
解答 解:(1)∵y=-3x2+12x-3=-3(x-2)2+9,
∴抛物线开口向下,对称轴为x=2,顶点坐标为(2,9),
其图象如图1所示:
(2)∵y=4x2-24x+26=4(x-3)2-10,
∴抛物线开口向上,对称轴为x=3,顶点坐标为(3,-10);
其图象如图2所示:
点评 本题考查了抛物线对称轴和抛物线的顶点坐标的求法,以及用描点法画函数图象,是基础知识,比较简单.

练习册系列答案
相关题目
13.如果一个三角形的两个外角之和为270°,那么这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=$4\sqrt{2}$,则梯形AECD的周长为( )
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=$4\sqrt{2}$,则梯形AECD的周长为( )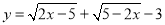 ,求2xy的值.
,求2xy的值.