题目内容
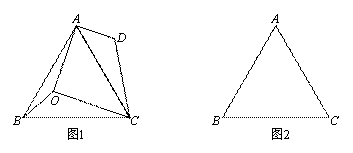
如右图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若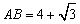 ,
,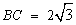 ,求⊙O的半径.
,求⊙O的半径.
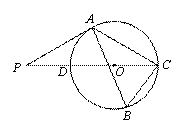
(1)证明:连接OA.
∵∠B=60°,
∴∠AOC=2∠B=120°.
又∵OA=OC,
∴∠OAC=∠OCA=30°.
又∵AP=AC,
∴∠P=∠ACP=30°.
∴∠OAP=∠AOC﹣∠P=90°.
∴OA⊥PA.
又∵点A在⊙O上,
∴PA是⊙O的切线.
(2)解:过点C作CE⊥AB于点E.
在Rt△BCE中,∠B=60°, ,
,
∴ ,CE=3. 分
,CE=3. 分
∵ ,
,
∴ .
.
∴在Rt△ACE中, .
.
∴AP=AC=5.
∴在Rt△PAO中, .
.
∴⊙O的半径为 .
.

练习册系列答案
相关题目
 中,已知a=12,h=8,S=120,则b= .
中,已知a=12,h=8,S=120,则b= . ,那么锐角
,那么锐角 的度数为 .
的度数为 . 
 ,
, 是反比例函数
是反比例函数 的图像上的两点,下列结论正确的是( )
的图像上的两点,下列结论正确的是( ) B.
B. C.
C. D.
D.
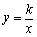 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数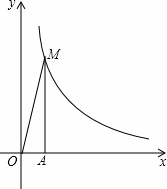
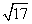 B.
B.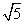 +2 C.3
+2 C.3