题目内容
已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
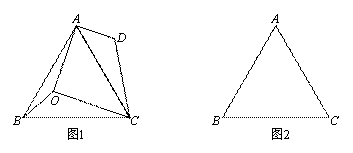
(1) 如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是 ;
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2) 设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.
解:(1)①90°.
②线段OA,OB,OC之间的数量关系是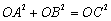 .
.
如图1,连接OD.
∵△BOC绕点C按顺时针方向旋转60°得△ADC,
 ∴△ADC≌△BOC,∠OCD=60°.
∴△ADC≌△BOC,∠OCD=60°.
∴CD = OC,∠ADC =∠BOC=120°, AD= OB.
∴△OCD是等边三角形.
∴OC=OD=CD,∠COD=∠CDO=60°.
∵∠AOB=150°,∠BOC=120°,
∴∠AOC=90°.
∴∠AOD=30°,∠ADO=60°.
∴∠DAO=90°.
在Rt△ADO中,∠DAO=90°,
∴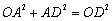 .
.
∴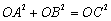 .
.
(2)①如图2,当α=β=120°时,OA+OB+OC有最小值.
作图如图2的实线部分.
如图2,将△AOC绕点C按顺时针方向旋转60°得△A’O’C,连接OO’.
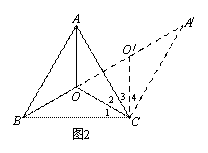 ∴△A’O’C≌△AOC,∠OCO’=∠ACA’=60°.
∴△A’O’C≌△AOC,∠OCO’=∠ACA’=60°.
∴O’C= OC, O’A’ = OA,A’C = BC,
∠A’O’C =∠AOC.
∴△OC O’是等边三角形.
∴OC= O’C = OO’,∠COO’=∠CO’O=60°.
∵∠AOB=∠BOC=120°,
∴∠AOC =∠A’O’C=120°.
∴∠BOO’=∠OO’A’=180°.
∴四点B,O,O’,A’共线.
∴OA+OB+OC= O’A’ +OB+OO’ =BA’ 时值最小.
②当等边△ABC的边长为1时,OA+OB+OC的最小值A’B=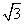 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 )÷3×|3﹣(﹣3)2|
)÷3×|3﹣(﹣3)2|
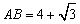 ,
,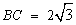 ,求⊙O的半径.
,求⊙O的半径.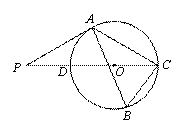
 的根的情况是( )
的根的情况是( ) ,当
,当 时,函数值y随自变量x的增大而减少,则m的取值范围是_________.
时,函数值y随自变量x的增大而减少,则m的取值范围是_________. 2 B.直线x=-2 C.直线x=4 D.直线x=-4
2 B.直线x=-2 C.直线x=4 D.直线x=-4 