题目内容
2.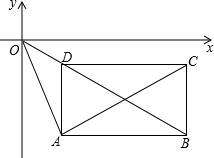 如图,矩形ABCD在平面直角坐标系内,AB∥CD∥x轴,AD∥BC∥x轴,点A、C都在双曲线$y=-\frac{1}{x}$上,且横坐标分别为a、c,线段AC=2AO.
如图,矩形ABCD在平面直角坐标系内,AB∥CD∥x轴,AD∥BC∥x轴,点A、C都在双曲线$y=-\frac{1}{x}$上,且横坐标分别为a、c,线段AC=2AO.(1)求直线OD的解析式(用含a、c的代数式表示);
(2)判断点B是否在直线OD上,并说明理由;
(3)如图,设M是x轴上一点,当∠DOM=25°时,求∠AOM的度数.
分析 (1)根据题意表示出A、C两点坐标,然后再表示出D点坐标,再设直线OD的解析式为y=kx,然后利用待定系数法可求出k,进而可得直线DO的解析式;
(2)根据A、C两点坐标,表示出B点坐标,再代入直线DO的解析式,能满足解析式,则B在直线OD上;
(3)首先根据矩形的性质可得AO′=CO′=$\frac{1}{2}$AC,BO′=AB,进而可得AO=AO′,进而可得∠3=∠4,然后再计算出∠1=∠2=25°,可得∠3的度数,从而可得∠4的度数,进而可得答案.
解答 解:(1)∵点A、C都在双曲线$y=-\frac{1}{x}$上,且横坐标分别为a、c,
∴A(a,-$\frac{1}{a}$),C(c,-$\frac{1}{c}$),
∵CD∥x轴,AD∥y轴,
∴D(a,-$\frac{1}{c}$),B(c,-$\frac{1}{a}$),
设直线OD的解析式为y=kx,
∴-$\frac{1}{c}$=ak,
解得:k=-$\frac{1}{ac}$,
∴OD的解析式为y=-$\frac{1}{ac}$x;
(2)∵当x=c时,y=-$\frac{1}{ac}$×c=-$\frac{1}{a}$,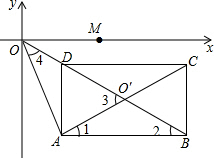
∴B在直线OD上;
(3)∵四边形ABCD是矩形,
∴AO′=CO′=$\frac{1}{2}$AC,BO′=AB,
∴∠1=∠2,
∵AB∥x轴,
∴∠2=∠MOD=25°,
∴∠1=25°,
∴∠3=50°,
∵AC=2AO,
∴AO′=AO,
∴∠3=∠4=50°,
∴∠MOA=25°+50°=75°.
点评 此题主要考查了反比例函数和矩形性质的应用,关键是正确表示出A、C两点坐标,从而得到D、B两点坐标,掌握凡是函数经过的点必能满足解析式,矩形对角线相等且互相平分.

练习册系列答案
相关题目
11.小李周末买进股票1000股,每股20元,下表为本周每日股票的涨跌情况:
(1)周四收盘时,小李所持股票每股多少元?
(2)本周内,股票最高价出现在星期几?是多少元?
(3)已知小李买进股票时付了购买金额1‰的手续费,卖出时需付成交额1‰的手续费和3‰的交易税.若小李在本周末卖出全部股票,他的收益如何?
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +1 | +4 | -1 | -2 | +1 |
(2)本周内,股票最高价出现在星期几?是多少元?
(3)已知小李买进股票时付了购买金额1‰的手续费,卖出时需付成交额1‰的手续费和3‰的交易税.若小李在本周末卖出全部股票,他的收益如何?
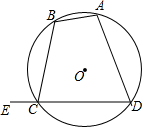 已知:如图,A,B,C,D为⊙O上的四个点,点E为DC延长线上的一点,求证:
已知:如图,A,B,C,D为⊙O上的四个点,点E为DC延长线上的一点,求证: 已知AB、BE、ED、CD依次相交于B、E、D,AB∥CD,试说明∠E=∠B+∠D.
已知AB、BE、ED、CD依次相交于B、E、D,AB∥CD,试说明∠E=∠B+∠D.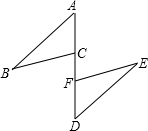 如图,A、C、F、D在同一直线上,AF=DC,CB=FE,∠ACB=110°,∠E=28°,BC∥EF
如图,A、C、F、D在同一直线上,AF=DC,CB=FE,∠ACB=110°,∠E=28°,BC∥EF