题目内容
7．试用一种方法推导多边形的内角和公式（n-2）×180°．分析 根据过同一顶点作出的对角线把多边形分成的三角形的个数的规律，再利用三角形的内角和等于180°即可推出多边形的内角和公式．
解答 解：n边形的内角和等于（n-2）•180°．（3分）
理由如下：如图：
∵三角形内角和 四边形内角和 五边形内角和 六边形内角和
180°×1 180°×2 180°×3 180°×4
∴过n边形某一顶点可画（n-3）条对角线，把n边形分为（n-2）个三角形，
这（n-2）个三角形的内角和之和就等于n边形的内角和，即（n-2）×180°．
点评 本题考查了多边形的内角和公式的推导，理清过同一个顶点把多边形分成的三角形的个数是解题的关键，也是本题的难点．
练习册系列答案
相关题目
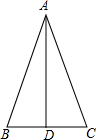如图，在△ABC中，AD平分∠BAC，AD平分BC．求证：△ABC是等腰三角形．
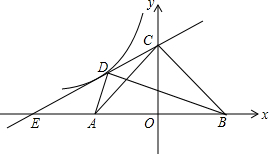如图，直线y=$\frac{1}{2}$x+2交坐标轴于E，C两点，A（-2，0），B（2，0），D为直线上一点，且AD⊥BD，反比例函数y=$\frac{k}{x}$（x＜0）经过D点．
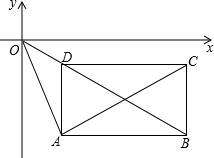如图，矩形ABCD在平面直角坐标系内，AB∥CD∥x轴，AD∥BC∥x轴，点A、C都在双曲线$y=-\frac{1}{x}$上，且横坐标分别为a、c，线段AC=2AO．
19．下列说法正确的是（ ）
| A． | 有刻度的直线是数轴 | |
| B． | 数轴上原点右侧的点表示的数都是正数 | |
| C． | 数轴上的点都表示有理数 | |
| D． | 在数轴上距离原点3个单位长度的点表示的数是3 |
16．下列各组数中，数值相等的是（ ）
| A． | 34和43 | B． | -32和（-3）2 | C． | -25和（-2）5 | D． | （-2×3）2和-22×32 |
17．
如图所示，在△ABC中，∠ACB=90°，D为AB中点，AC=6，DC=5，则△ABC的面积为（ ）
如图所示，在△ABC中，∠ACB=90°，D为AB中点，AC=6，DC=5，则△ABC的面积为（ ）| A． | 21 | B． | 22 | C． | 23 | D． | 24 |