Question

.如图，⊙O是△ABC的外接圆，AB是⊙O的直径，FO⊥AB，垂足为点O，连接AF并延长交⊙O于点D，连接OD交BC于点E，∠B=30°，FO=2．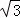

（1）求AC的长度；

（2）求图中阴影部分的面积．（计算结果保留根号）

　

 

Answer 1

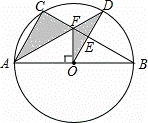
       解：（1）∵OF⊥AB，

∴∠BOF=90°，

∵∠B=30°，FO=2，

∴OB=6，AB=2OB=12，

又∵AB为⊙O的直径，

∴∠ACB=90°，

∴AC=AB=6；

（2）∵由（1）可知，AB=12，

∴AO=6，即AC=AO，

在Rt△ACF和Rt△AOF中，

∴Rt△ACF≌Rt△AOF，

∴∠FAO=∠FAC=30°，

∴∠DOB=60°，

过点D作DG⊥AB于点G，

∵OD=6，∴DG=3，

∴S_△ACF+S_△OFD=S_△AOD=×6×3=9，

即阴影部分的面积是9．