题目内容
如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
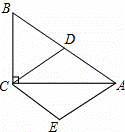
(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
又∵∠ACB=90°,D是AB的中点,
∴CD= AB=BD=AD,
AB=BD=AD,
∴平行四边形ADCE是菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
∴在Rt△CDF中,DF=CD1sin60°=6× =3
=3 .
.


练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 ,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大? ≌
≌ 。(只需写一个)
。(只需写一个)
 :
: C. 4:9 D. 8:27
C. 4:9 D. 8:27 化简的结果为 .
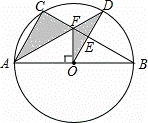
化简的结果为 .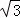 .
.

 B.
B.  C.
C.  D.
D. 
