题目内容
如图,在△ABC中,AB=5,BC=3,AC=4,动点E(与点A、C不重合)在AC边上,EF∥AB交BC于点F.
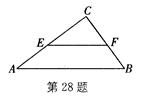
小题1:当△ECF的面积与四边形EABF的面积相等时,求CE的长
小题2:当△ECF的周长与四边形EABF的周长相等时,求CE的长
小题3:试问在AB上是否存在点P,使得△EFP为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出EF的长.

小题1:当△ECF的面积与四边形EABF的面积相等时,求CE的长
小题2:当△ECF的周长与四边形EABF的周长相等时,求CE的长
小题3:试问在AB上是否存在点P,使得△EFP为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出EF的长.
小题1:CE=2
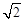
小题2:
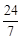
小题3:在AB上存在点P.使△EFP为等腰直角三角形,此时EF=
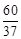 或EF=
或EF=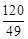
解:(1)∵△ECF的面积与四边形EABF的面积相等,
∴S△ECF:S△ACB=1:2,
又∵EF∥AB,∴△ECF∽△ACB,
∴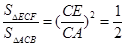 ,且AC=4,
,且AC=4,
∴CE=2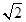 ;
;
(2)设CE的长为x,
∵△ECF∽△ACB,
∴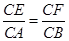 ,∴CF=
,∴CF= x,
x,
由△ECF的周长与四边形EABF的周长相等,得:
x+EF+ x=(4-x)+5+(3-
x=(4-x)+5+(3- x)+EF
x)+EF
解得x=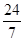 ,∴CE的长为
,∴CE的长为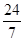
(3)△EFP为等腰直角三角形,有两种情况:
①如图1,假设∠PEF=90°,EP=EF
由AB=5,BC=3,AC=4,得∠C=90°
∴Rt△ACB斜边AB上高CD=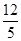 ,设EP=EF=x,由△ECF∽△ACB,得:
,设EP=EF=x,由△ECF∽△ACB,得:
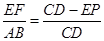
即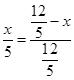 ,
,
解得x=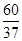 ,即EF=
,即EF=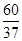
当∠EFP´=90°,EF=FP′时,同理可得EF=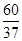 ;
;
②如图2,假设∠EPF=90°,PE=PF时,点P到EF的距离为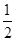 EF
EF
设EF=x,由△ECF∽△ACB,得:

解得x=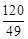 ,即EF=
,即EF=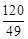
综上所述,在AB上存在点P,使△EFP为等腰直角三角形,此时EF=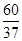 或EF=
或EF=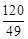
∴S△ECF:S△ACB=1:2,
又∵EF∥AB,∴△ECF∽△ACB,
∴
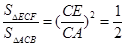 ,且AC=4,
,且AC=4,∴CE=2
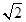 ;
;(2)设CE的长为x,
∵△ECF∽△ACB,
∴
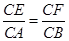 ,∴CF=
,∴CF= x,
x,由△ECF的周长与四边形EABF的周长相等,得:
x+EF+
 x=(4-x)+5+(3-
x=(4-x)+5+(3- x)+EF
x)+EF解得x=
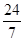 ,∴CE的长为
,∴CE的长为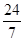
(3)△EFP为等腰直角三角形,有两种情况:
①如图1,假设∠PEF=90°,EP=EF
由AB=5,BC=3,AC=4,得∠C=90°
∴Rt△ACB斜边AB上高CD=
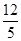 ,设EP=EF=x,由△ECF∽△ACB,得:
,设EP=EF=x,由△ECF∽△ACB,得: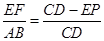
即
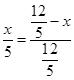 ,
,解得x=
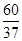 ,即EF=
,即EF=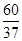
当∠EFP´=90°,EF=FP′时,同理可得EF=
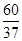 ;
;②如图2,假设∠EPF=90°,PE=PF时,点P到EF的距离为
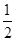 EF
EF设EF=x,由△ECF∽△ACB,得:

解得x=
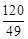 ,即EF=
,即EF=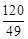
综上所述,在AB上存在点P,使△EFP为等腰直角三角形,此时EF=
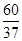 或EF=
或EF=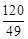

练习册系列答案
相关题目
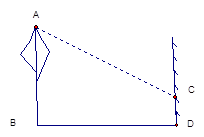
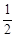 ∠CAB.
∠CAB.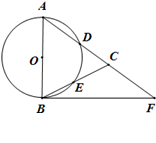
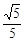 ,求BC和BF的长.
,求BC和BF的长.
 .
.
 ;
; °时,求证:
°时,求证: .
.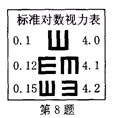
 应为 【 ▲ 】
应为 【 ▲ 】
 是直角三角形,
是直角三角形, ,点
,点 的坐标分别为
的坐标分别为 ,
,
 的直线的函数表达式
的直线的函数表达式 轴上找一点
轴上找一点 ,连接
,连接 ,使得
,使得 与
与 分别是
分别是 和
和 上的动点,连接
上的动点,连接 ,设
,设 ,问是否存在这样的
,问是否存在这样的 使得
使得 与
与