题目内容
已知:如图,在平面直角坐标系中, 是直角三角形,
是直角三角形, ,点
,点 的坐标分别为
的坐标分别为 ,
,
小题1:求过点 的直线的函数表达式
的直线的函数表达式
小题2:在 轴上找一点
轴上找一点 ,连接
,连接 ,使得
,使得 与
与 相似(不包括全等),并求点
相似(不包括全等),并求点 的坐标;
的坐标;
小题3:在⑵的条件下,如 分别是
分别是 和
和 上的动点,连接
上的动点,连接 ,设
,设 ,问是否存在这样的
,问是否存在这样的 使得
使得 与
与 相似,如果存在,请求出
相似,如果存在,请求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
 是直角三角形,
是直角三角形, ,点
,点 的坐标分别为
的坐标分别为 ,
,
小题1:求过点
 的直线的函数表达式
的直线的函数表达式小题2:在
 轴上找一点
轴上找一点 ,连接
,连接 ,使得
,使得 与
与 相似(不包括全等),并求点
相似(不包括全等),并求点 的坐标;
的坐标;小题3:在⑵的条件下,如
 分别是
分别是 和
和 上的动点,连接
上的动点,连接 ,设
,设 ,问是否存在这样的
,问是否存在这样的 使得
使得 与
与 相似,如果存在,请求出
相似,如果存在,请求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.小题1:∵点A(-3,0),C(1,0),
∴AC=4,BC=tan∠BAC×AC=
 ×4=3,B点坐标为(1,3),
×4=3,B点坐标为(1,3),设过点A,B的直线的函数表达式为y=kx+b,
由 0=k×(-3)+b ,
3=k+b
解得k=
 ,b=
,b= ,
,∴直线AB的函数表达式为y=
 x+
x+
小题2:如图,过点B作BD⊥AB,交x轴于点D,
在Rt△ABC和Rt△ADB中,
∵∠BAC=∠DAB,
∴Rt△ABC∽Rt△ADB,
∴D点为所求,
又tan∠ADB=tan∠ABC=
 ,
,∴CD=BC÷tan∠ADB=3÷
 =
= ,
,∴OD=OC+CD=
 ,∴D(
,∴D( ,0);
,0);小题3:这样的m存在.
在Rt△ABC中,由勾股定理得AB=5,
如图1,
当PQ∥BD时,△APQ∽△ABD,则
 ,
,解得m=
 ,
,如图2,
当PQ⊥AD时,△APQ∽△ADB,
则

解得m=
 .
.主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 于点E,DA平分
于点E,DA平分 .
. 

 C.
C. D.4
D.4
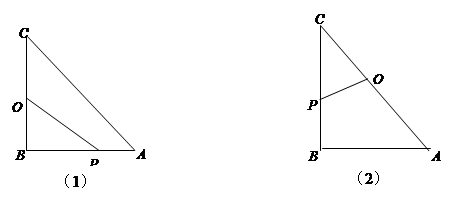
 的边AC上的一点,连结BP,则下列条件中不能判定
的边AC上的一点,连结BP,则下列条件中不能判定 ∽
∽ 的是( )
的是( ) 




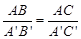 ,∠A=∠B'
,∠A=∠B'