题目内容
 △ABC内接于⊙O,CD⊥AB于点D,M为
△ABC内接于⊙O,CD⊥AB于点D,M为 |
| AB |
(1)求证:∠ACD=∠BCO;
(2)过M作ME⊥BC于E,若∠ACB=60°,S四边形ACBM=
| 3 |
考点:圆周角定理,全等三角形的判定与性质,圆心角、弧、弦的关系
专题:
分析:(1)延长CO到⊙O上一点F,连接FB,利用圆周角定理得出∠FBC=90°,进而得出答案;
(2)首先过点M作MQ⊥CA延长线于点Q,得出Rt△QAM≌Rt△BEM(HL),进而得出Rt△QCM≌Rt△ECM(HL),求出S△QCM=S△ECM=
,进而得出即可.
(2)首先过点M作MQ⊥CA延长线于点Q,得出Rt△QAM≌Rt△BEM(HL),进而得出Rt△QCM≌Rt△ECM(HL),求出S△QCM=S△ECM=
| ||
| 2 |
解答: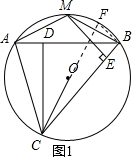 (1)证明:如图1,延长CO到⊙O上一点F,连接FB,
(1)证明:如图1,延长CO到⊙O上一点F,连接FB,
∵FC是⊙O直径,
∴∠FBC=90°,
∵∠CFB=∠CAB,∠ADC=∠CBF=90°,
∴∠ACD=∠BCO;
(2)解:如图2:
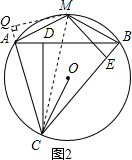
过点M作MQ⊥CA延长线于点Q,
∵M为
的中点,
∴
=
,
∴AM=BM,∠ACM=∠BCM=30°,
∵MQ⊥AC,ME⊥BC,∠ACM=∠BCM,
∴QM=ME,
在Rt△QAM和Rt△BEM中
∵
,
∴Rt△QAM≌Rt△BEM(HL),
∴S四边形ACBM=S四边形QCEM=
,
在Rt△QCM和Rt△ECM中
∵
∴Rt△QCM≌Rt△ECM(HL),
∴S△QCM=S△ECM=
,
设EC=x,则
=tan30°=
,故ME=
EC=
x,
则
×x×
x=
,
解得:x=±
(负数舍去),
即EC的长为
.
 (1)证明:如图1,延长CO到⊙O上一点F,连接FB,
(1)证明:如图1,延长CO到⊙O上一点F,连接FB,∵FC是⊙O直径,
∴∠FBC=90°,
∵∠CFB=∠CAB,∠ADC=∠CBF=90°,
∴∠ACD=∠BCO;
(2)解:如图2:

过点M作MQ⊥CA延长线于点Q,
∵M为
 |
| AB |
∴
 |
| AM |
 |
| BM |
∴AM=BM,∠ACM=∠BCM=30°,
∵MQ⊥AC,ME⊥BC,∠ACM=∠BCM,
∴QM=ME,
在Rt△QAM和Rt△BEM中
∵
|
∴Rt△QAM≌Rt△BEM(HL),
∴S四边形ACBM=S四边形QCEM=
| 3 |
在Rt△QCM和Rt△ECM中
∵
|
∴Rt△QCM≌Rt△ECM(HL),
∴S△QCM=S△ECM=
| ||
| 2 |
设EC=x,则
| ME |
| EC |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
则
| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
解得:x=±
| 3 |
即EC的长为
| 3 |
点评:此题主要考查了圆周角定理以及全等三角形的判定与性质以及角平分线的性质等知识,得出S△QCM=S△ECM=
是解题关键.
| ||
| 2 |

练习册系列答案
相关题目
若※是新规定的运算符号,设a※b=a2-b,则3※12的值是( )
| A、-6 | B、-3 | C、15 | D、21 |
已知正比例函数y=kx,当x=2时,y=-3,则它的表达式为( )
A、y=-
| ||
B、y=
| ||
C、y=
| ||
D、y=-
|
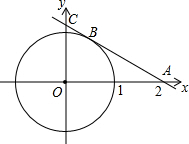 如图,⊙O的半径为1,经过点A(2,0)的直线与⊙O相切于点B,与y轴相交于点C.
如图,⊙O的半径为1,经过点A(2,0)的直线与⊙O相切于点B,与y轴相交于点C.