题目内容
1.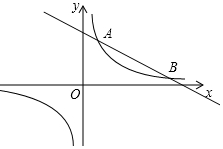 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).(1)求反比例函数与一次函数的表达式;
(2)点C为x轴上一个动点,若S△ABC=10,求点C的坐标.
分析 (1)把点A的坐标代入y=$\frac{m}{x}$,求出反比例函数的解析式,把点B的坐标代入y=$\frac{12}{x}$,得出n的值,得出点B的坐标,再把A、B的坐标代入直线y=kx+b,求出k、b的值,从而得出一次函数的解析式;
(2)如图,直线AB与x轴的交点为E,设点C的坐标为(m,0),连接AC,BC,则点P的坐标为(14,0).CE=|m-14|.根据S△ACB=S△ACE-S△BCE=10,列出方程,求出m的值,从而得出点E的坐标;
解答 解:(1)把点A(2,6)代入y=$\frac{m}{x}$,得m=12,
则y=$\frac{12}{x}$.
把点B(n,1)代入y=$\frac{12}{x}$,得n=12,
则点B的坐标为(12,1).
由直线y=kx+b过点A(2,6),点B(12,1)得$\left\{\begin{array}{l}{2k+b=6}\\{12k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=7}\end{array}\right.$,
则所求一次函数的表达式为y=-$\frac{1}{2}$x+7.
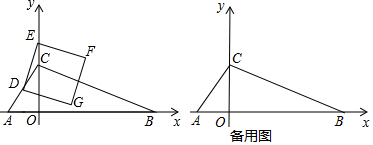
(2)如图,直线AB与x轴的交点为E,设点C的坐标为(m,0),连接AC,BC,
则点P的坐标为(14,0).
∴CE=|m-14|.
∵S△ACB=S△ACE-S△BCE=10,
∴$\frac{1}{2}$×|m-14|×(6-1)=10.
∴|m-14|=4.
∴m1=18,m2=10.
∴点E的坐标为(18,0)或(10,0).
点评 此题考查了反比例函数和一次函数的交点问题,用待定系数法求一次函数和反比例函数的解析式,三角形的面积,解一元一次方程,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

| A. | 平移和旋转都不改变图形的形状和大小 | |
| B. | 成中心对称的两个图形中,对应点连线的中点是对称中心 | |
| C. | 在平移和旋转图形的过程中,对应角相等,对应线段相等且平行 | |
| D. | 一个图形和它经过旋转后所得的图形中,对应点到旋转中心的距离相等 |
| A. | -3 | B. | 2 | C. | 0 | D. | -1 |
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
 下面空心圆柱形物体的左视图是( )
下面空心圆柱形物体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | 从一个装满黑球的布袋中摸出一个球是黑球 | |
| B. | 抛掷1枚普通硬币得到正面朝上 | |
| C. | 抛掷1颗正方体骰子得到的点数是偶数 | |
| D. | 抛掷1个普通图钉一定是针尖向下 |
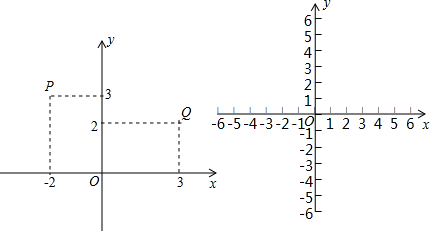
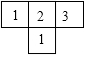 由7个大小相同的小正方体组合成一个几何体.其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )
由7个大小相同的小正方体组合成一个几何体.其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )