题目内容
求直线y=2x+3与直线y=-x+6的交点坐标,并求出两直线与x轴所围成的三角形的面积.分析:两直线相交时,y值相等,故可得2x+3=-x+6,解得x的值后再把x值代入任何一个解析式都可得到y的值,即可得到交点坐标;画出两函数图象,根据所画的图象,可知两直线与x轴所围成的三角形,求出△ABE的面积即可.
解答: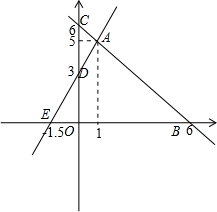 解:∵直线y=2x+3与直线y=-x+6相交,
解:∵直线y=2x+3与直线y=-x+6相交,
∴2x+3=-x+6,
解得:x=1,
把x=1代入y=-x+6中得:
y=-1+6=5,
∴直线y=2x+3与直线y=-x+6的交点坐标是:(1,5),
S△ABE=
×BE×5=
×7.5×5=
.
 解:∵直线y=2x+3与直线y=-x+6相交,
解:∵直线y=2x+3与直线y=-x+6相交,∴2x+3=-x+6,
解得:x=1,
把x=1代入y=-x+6中得:
y=-1+6=5,
∴直线y=2x+3与直线y=-x+6的交点坐标是:(1,5),
S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 75 |
| 4 |
点评:此题主要考查了画一次函数图象,求两直线交点坐标以及求三角形面积问题,画一次函数y=kx+b图象根据两点(0,b)(-
,0)即可;此题易错点在求两直线与x轴所围成的三角形的面积上,很多同学只求△ABE的面积,而漏掉了△ACD的面积.
| b |
| k |

练习册系列答案
相关题目
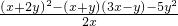 ,其中x=-2,
,其中x=-2,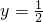 ;
;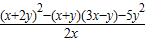 ,其中x=-2,
,其中x=-2,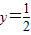 ;
;