题目内容
(1)先化简,再求值: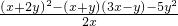 ,其中x=-2,
,其中x=-2,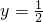 ;
;
(2)求直线y=2x+1与抛物线y=3x2+3x-1的交点坐标.
解:(1)原式=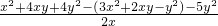
=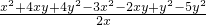
=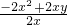
=-x+y
当x=-2,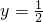 时原式=
时原式=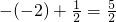 ;
;
(2)联立y=2x+1和y=3x2+3x-1,可得2x+1=3x2+3x-1,
化简可得3x2+x-2=0
解方程,得x1=-1,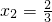 ,
,
当x1=-1时,y1=-1,
则一交点为(-1,-1);
当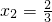 时,y2=
时,y2= ,
,
则另一交点为 ,
,
综上所述,直线y=2x+1与抛物线y=3x2+3x-1的交点坐标为
(-1,-1),
分析:(1)先利用分式的运算法则化简,再代数求值;
(2)函数图象的交点坐标对应的是两个函数解析式联立成方程组的解.
点评:主要考查了分式的化简求值和函数图象交点的意义和求法.
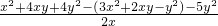
=
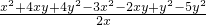
=
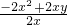
=-x+y
当x=-2,
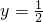 时原式=
时原式=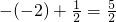 ;
;(2)联立y=2x+1和y=3x2+3x-1,可得2x+1=3x2+3x-1,
化简可得3x2+x-2=0
解方程,得x1=-1,
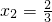 ,
,当x1=-1时,y1=-1,
则一交点为(-1,-1);
当
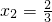 时,y2=
时,y2= ,
,则另一交点为
 ,
,综上所述,直线y=2x+1与抛物线y=3x2+3x-1的交点坐标为
(-1,-1),

分析:(1)先利用分式的运算法则化简,再代数求值;
(2)函数图象的交点坐标对应的是两个函数解析式联立成方程组的解.
点评:主要考查了分式的化简求值和函数图象交点的意义和求法.

练习册系列答案
相关题目