题目内容
一列数a1,a2,a3,…an,其中a1=-1,a2=
,a3=
,…,an=
,则a1+a2+a3+…+a2014= .
| 1 |
| 1-a1 |
| 1 |
| 1-a2 |
| 1 |
| 1-an-1 |
考点:规律型:数字的变化类
专题:规律型
分析:分别求得a1、a2、a3、…,找出数字循环的规律,进一步利用规律解决问题.
解答:解:a1=-1,
a2=
=
,
a3=
=2,
a4=
=-1,
…,
由此可以看出三个数字一循环,
∵2014÷3=671…1,
∴a1+a2+a3+…+a2014=671×(-1+
+2)-1=1005.5.
故答案为:1005.5.
a2=
| 1 |
| 1-a1 |
| 1 |
| 2 |
a3=
| 1 |
| 1-a2 |
a4=
| 1 |
| 1-a3 |
…,
由此可以看出三个数字一循环,
∵2014÷3=671…1,
∴a1+a2+a3+…+a2014=671×(-1+
| 1 |
| 2 |
故答案为:1005.5.
点评:此题考查了找规律,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,找出规律是解题的关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知一次函数y=-2x+1,当-1≤y<3时,自变量的取值范围是( )
| A、-1≤x<1 |
| B、-1<x≤1 |
| C、-2<x≤2 |
| D、-2≤x<2 |
(3a-bc)(-bc-3a)等于( )
| A、bc-9a2 |
| B、b2c2-3a2 |
| C、9a2-b2c2 |
| D、b2c2-9a2 |
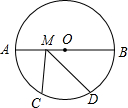 在⊙O中,AB是⊙O的直径,AB=8cm,
在⊙O中,AB是⊙O的直径,AB=8cm,
 小明把如图所示的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是( )
小明把如图所示的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是( )