Question

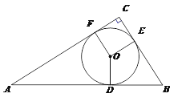
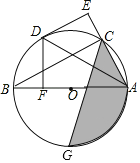
【题目】如图，AB是⊙O的直径，C为⊙O上一点，点D是 的中点，DE是⊙O的切线，DF⊥AB于F，点G是 的中点

（1）求证：△ADE≌△ADF；

（2）若OF＝3，AB＝10，求图中阴影部分的面积．

Answer 1

【答案】（1）详见解析；（2） ．

【解析】

（1）连接OD，证明DE∥BC，进而得∠E＝∠DFA＝∠ACB＝90°，由D是 的中点得∠DAE＝∠DAF，再结合公共边，由AAS定理得结论；

（2）连接OD，OG，过O作OH⊥AC于H，过C作CK⊥OA于点K，由勾股定理求得 DF，便可得OH，再求AH，AK，再由相似三角形求得OM，最后求出扇形OAG，△OGM和△ACM的面积便可．

（1）证明：连接OD，如图1，

∵点D是的中点，

∴∠DAF＝∠DAE，OD⊥BC，

∵DE是⊙O的切线，

∴OD⊥DE，

∴DE∥BC，

∵AB是⊙O的直径，

∴∠ACB＝90°，

∴∠AED＝∠ACB＝90°，

∵AD＝AD，

∴：△ADE≌△ADF（AAS）；

（2）连接OD，OG，过O作OH⊥AC于H，过C作CK⊥OA于点K，如图2，

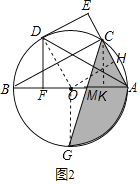
则AH＝CH，∠GOA＝∠GOB＝90°，OA＝OB＝OD＝5，

∴OH＝DE＝DF＝ ，

∴CH＝AH＝ ，

∴BC＝ ，

∵ ，

∴CK＝ ，

∴AK＝

∴OK＝OA﹣AK＝ ，

∵OG∥CK，

∴△OGM∽△KCM，

∴ ，

即 ，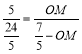

∴OM＝ ，

∴AM＝5﹣ ，

∴ ，

，

∴