题目内容
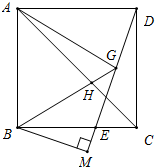 在正方形ABCD中,点E为BC边上的一点,连接DE,点G为DE中点,连接GA、GB、GC,GB与AC交于点H,过点B作BM垂直DE延长线于点M.
在正方形ABCD中,点E为BC边上的一点,连接DE,点G为DE中点,连接GA、GB、GC,GB与AC交于点H,过点B作BM垂直DE延长线于点M.(1)求证:GA=GB;
(2)若AH=
| 3 |
| 2 |
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质求得AD=BC,∠BCD=90°,然后根据直角三角形斜边上中线的性质求得CG=GE=GD,∠GCD=∠GDC,根据等量减等量求得∠BCG=∠ADG,根据SAS求得△ADG≌△BCG,从而证得GA=GB.
(2)过点H作HN⊥BC于N,根据正方形的性质可得△CHN为等腰直角三角形,根据等腰直角三角形的性质可得HN=CN,再根据平行线分线段成比例定理求出
=
,即
=
,然后求出∠HBN=30°,然后判断出△ABG是等边三角形,再求出∠AGD=75°,然后根据平角等于180°求出∠BGM=45°,再根据等腰直角三角形的斜边等于直角边的
证明即可.
(2)过点H作HN⊥BC于N,根据正方形的性质可得△CHN为等腰直角三角形,根据等腰直角三角形的性质可得HN=CN,再根据平行线分线段成比例定理求出
| BN |
| CN |
| 3 |
| HN |
| BN |
| 3 |
| 2 |
解答:(1)证明:∵四边形ABCD是正方形,
∴AD=BC,∠BCD=90°,
又∵点G为DE中点,
∴CG=GE=GD,
∴∠GCD=∠GDC,
∴∠BCG=∠ADG,
在△ADG与△BCG中,
,
∴△ADG≌△BCG(SAS),
∴GA=GB.
 (2)证明:如图,过点H作HN⊥BC于N,
(2)证明:如图,过点H作HN⊥BC于N,
∵AC是正方形ABCD的对角线,
∴∠ACB=45°,
∴△CHN为等腰直角三角形,
∴HN=CN,
易得AB∥HN,
∴
=
=
,
∴
=
,
∴∠HBN=30°,
∵∠ABC=90°,
∴∠ABG=90°-30°=60°,
∴△ABG是等边三角形,
由(1)知GA=GB,
∴AD=AG=AB,
∴∠AGD=
(180°-30°)=75°,
∴∠BGM=180°-75°-60°=45°,
∵BM⊥E,
∴△BMG是等腰直角三角形,
∴BG=
BM,
∴AG=
BM.
∴AD=BC,∠BCD=90°,
又∵点G为DE中点,
∴CG=GE=GD,
∴∠GCD=∠GDC,
∴∠BCG=∠ADG,
在△ADG与△BCG中,
|
∴△ADG≌△BCG(SAS),
∴GA=GB.
 (2)证明:如图,过点H作HN⊥BC于N,
(2)证明:如图,过点H作HN⊥BC于N,∵AC是正方形ABCD的对角线,
∴∠ACB=45°,
∴△CHN为等腰直角三角形,
∴HN=CN,
易得AB∥HN,
∴
| BN |
| CN |
| AH |
| CH |
| 3 |
∴
| HN |
| BN |
| 3 |
∴∠HBN=30°,
∵∠ABC=90°,
∴∠ABG=90°-30°=60°,
∴△ABG是等边三角形,
由(1)知GA=GB,
∴AD=AG=AB,
∴∠AGD=
| 1 |
| 2 |
∴∠BGM=180°-75°-60°=45°,
∵BM⊥E,
∴△BMG是等腰直角三角形,
∴BG=
| 2 |
∴AG=
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,等边三角形的判定与性质,难点在于(2)作辅助线构造出等腰直角三角形和含30°角的直角三角形,求出∠HBN=30°是本题的难点,也是关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
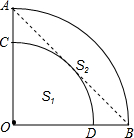 如图,∠AOB=90°,
如图,∠AOB=90°, |
| AB |
 |
| CD |
 |
| CD |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、不确定 |
 如图所示,截去正方体一角变成一个新的多面体,这个新多面体有7个顶点,有
如图所示,截去正方体一角变成一个新的多面体,这个新多面体有7个顶点,有