Question

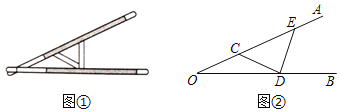
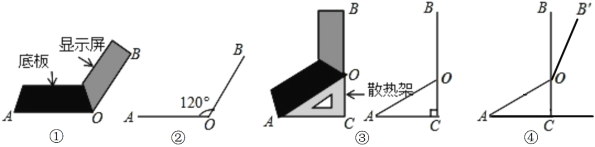
【题目】小华同学将笔记本电脑水平放置在桌子上，当是示屏的边缘线与底板的边缘线所在水平线的夹角为120°时，感觉最舒适（如图①）．侧面示意图为图②；使用时为了散热，他在底板下面垫入散热架，如图③，点、、在同一直线上，，，．

（1）求的长；

（2）如图④，垫入散热架后，要使显示屏的边缘线与水平线的夹角仍保持120°，求点到的距离．（结果保留根号）

Answer 1

【答案】（1）12cm；（2）点到的距离为（12+12）cm．

【解析】

（1）在Rt△AOC中，由30度角所对的直角边长度是斜边的一半求解即可；

（2）过点O作OM∥AC，过点B′作B′E⊥AC交AC的延长线于点E，交OM于点D，B′E即为点到的距离，根据题意求出∠OB′D=30°，四边形OCED为矩形，根据B′E=B′D+DE求解即可．

解：（1）∵，，

∴．

即OC的长度为12cm．

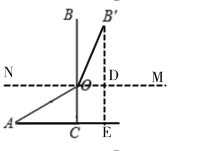
（2）如图，过点O作OM∥AC，过点B′作B′E⊥AC交AC的延长线于点E，交OM于点D，B′E即为点到的距离，

∵OM∥AC，B′E⊥AC，

∴B′E⊥OD，

∵MN∥AC，

∴∠NOA=∠OAC=30°，

∵∠AOB=120°，

∴∠NOB=90°，

∵∠NOB′=120°，

∴∠BOB′=120°-90°=30°，

∵BC⊥AC，B′E⊥AE，MN∥AE，

∴BC∥B′E，四边形OCED为矩形，

∴∠OB′D=∠BOB′=30°，DE=OC=12cm，

在Rt△B′OD中，∵∠OB′D=30°，B′O=BO=24cm，

∴

B′D= ，

B′E=B′D+DE= ，

答：点到的距离为．