题目内容
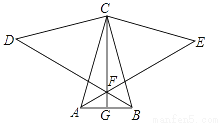
如图,在等腰三角形ABC中,AC=BC,分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE,AE与BD相交于点F,连接CF并延长交AB于点G.求证:CG垂直平分AB.
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
题目内容
如图,在等腰三角形ABC中,AC=BC,分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE,AE与BD相交于点F,连接CF并延长交AB于点G.求证:CG垂直平分AB.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案