题目内容
4.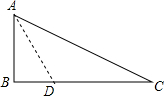 如图,有一块直角三角形纸片,两直角边长AB=6,BC=8,将直角边AB折叠,使它落在斜边AC上,折痕为AD,则CD长是( )
如图,有一块直角三角形纸片,两直角边长AB=6,BC=8,将直角边AB折叠,使它落在斜边AC上,折痕为AD,则CD长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 设点B落在AC上的E点处,连接DE,如图所示,由三角形ABC为直角三角形,已知AB与BC的长,利用勾股定理求出AC的长,设BD=x,由折叠的性质得到ED=BD=x,AE=AB=6,进而表示出CE与CD,在直角三角形DEC中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,进而得到CD的长.
解答  解:设点B落在AC上的E点处,连接DE,如图所示,
解:设点B落在AC上的E点处,连接DE,如图所示,
∵△ABC为直角三角形,AB=6,BC=8,
∴根据勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10.
设BD=x,由折叠可知:DE=BD=x,AE=AB=6,
可得:CE=AC-AE=10-6=4,CD=BC-BD=8-x,
在Rt△CDE中,根据勾股定理得:(8-x)2=42+x2,
解得:x=3,
∴CD=8-3=5.
故选C.
点评 本题主要考查了翻折变换、勾股定理等知识点,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
15.下列命题中假命题的是( )
| A. | 同位角相等 | |
| B. | 同旁内角互补,两直线平行 | |
| C. | 等角的余角相等 | |
| D. | 过一点能且只能作一条直线和直线平行 |
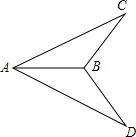 如图,已知AC=AD,∠CAB=∠DAB,求证:∠C=∠D.
如图,已知AC=AD,∠CAB=∠DAB,求证:∠C=∠D. 已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)
已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)