题目内容
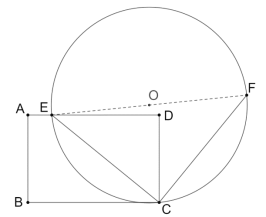
【题目】如图,四边形ABCD内接于⊙O,AC为直径,点D为弧ACB的中点,过点D的切线与BC的延长线交于点E.
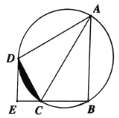
(1)用尺规作图作出圆心O;(保留作图痕迹,不写作法);
(2)求证:DE⊥BC;
(3)若OC=2CE=4,求图中阴影部分面积.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)如图做出AC的垂直平分线交点即为所求;
(2)连接![]() 并延长交
并延长交![]() 于点
于点![]() ,由
,由![]() 是
是![]() 的切线,
的切线,![]() 是
是![]() 的直径,
的直径,![]() 是优弧
是优弧![]() 的中点,证明四边形
的中点,证明四边形![]() 为矩形即可;
为矩形即可;
(3)过点![]() 作
作![]() 于点
于点![]() ,证明
,证明![]() 垂直平分
垂直平分![]() ,再求证出
,再求证出![]() 的等边三角形即可求阴影面积.
的等边三角形即可求阴影面积.
解:(1)圆心![]() 如图所示
如图所示

(2)连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,

∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∵![]() 是优弧
是优弧![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴![]() .
.
(3)过点![]() 作
作![]() 于点
于点![]() ,则四边形
,则四边形![]() 是矩形,
是矩形,

∴![]() ,
,
∴![]() ,
,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
∴![]() 的等边三角形,
的等边三角形,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目