题目内容
17.定义一种新运算:观察下列各式:1⊙3=1×4+3=7 3⊙(-1)=3×4-1=11 5⊙4=5×4+4=24 4⊙(-3)=4×4-3=13
(1)请你想一想:a⊙b=4a+b;
(2)若a≠b,那么a⊙b≠b⊙a(填入“=”或“≠”)
(3)若a⊙(-2b)=4,则2a-b=2;请计算(a-b)⊙(2a+b)的值.
分析 (1)根据题目中的式子可以猜出a⊙b的结果;
(2)根据(1)中的结果和a≠b,可以得到a⊙b和b⊙a的关系;
(3)根据(1)中的结果可以得到2a-b的值以及计算出(a-b)⊙(2a+b)的值,
解答 解:(1)由题目中的式子可得,
a⊙b=4a+b,
故答案为:4a+b;
(2)∵a⊙b=4a+b,b⊙a=4b+a,
∴(a⊙b)-(b⊙a)
=(4a+b)-(4b+a)
=4a+b-4b-a
=4(a-b)+(b-a),
∵a≠b,
∴4(a-b)+(b-a)≠0,
∴(a⊙b)≠(b⊙a),
故答案为:≠;
(3)a⊙(-2b)=4,a⊙(-2b)=4a+(-2b)=4a-2b,
∴4=4a-2b,
∴2a-b=2,
故答案为:2;
(a-b)⊙(2a+b)
=4(a-b)+(2a+b)
=4a-4b+2a+b
=6a-3b
=3(2a-b)
=3×2
=6.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.

练习册系列答案
相关题目
8.根据国家旅游局数据中心综合测算,今年国庆期间全国累计旅游收入4 822亿元,用科学记数法表示4 822亿正确的是( )
| A. | 4822×108 | B. | 4.822×1011 | C. | 48.22×1010 | D. | 0.4822×1012 |
5.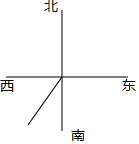 如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )
如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )
 如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )
如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )| A. | 南偏东40°方向 | B. | 北偏西50°方向 | C. | 南偏东50°方向 | D. | 东南方向 |
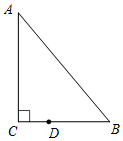 如图,Rt△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把线段BD 绕着点D逆时针旋转α(0<α<180)度后,如果点B恰好落在Rt△ABC的边上,那么α=70°或120°.
如图,Rt△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把线段BD 绕着点D逆时针旋转α(0<α<180)度后,如果点B恰好落在Rt△ABC的边上,那么α=70°或120°.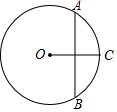 如图,在半径为10的⊙O中,垂直平分半径的弦AB的长为$10\sqrt{3}$.
如图,在半径为10的⊙O中,垂直平分半径的弦AB的长为$10\sqrt{3}$.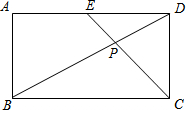 学完第五章《平面直角坐标系》和第六章《一次函数》后,老师布置了这样一道思考题:
学完第五章《平面直角坐标系》和第六章《一次函数》后,老师布置了这样一道思考题:
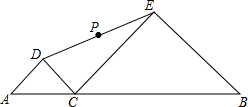 如图,线段AB长为6cm,点C是线段AB上一动点(不与A,B重合),分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1cm处沿AB向右运动至距离B点1cm处时,点P运动的路径长是2cm.
如图,线段AB长为6cm,点C是线段AB上一动点(不与A,B重合),分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1cm处沿AB向右运动至距离B点1cm处时,点P运动的路径长是2cm.