题目内容
2.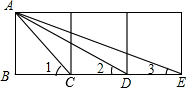 三个正方形如图排列,AC,AD,AE为三条对角线,求∠1+∠2+∠3的度数.
三个正方形如图排列,AC,AD,AE为三条对角线,求∠1+∠2+∠3的度数.
分析 设正方形的边长为1,根据正方形的性质得AC=$\sqrt{2}$,CD=1,CE=2,则可计算出$\frac{CD}{AC}$=$\frac{AC}{CE}$=$\frac{\sqrt{2}}{2}$,加上∠ACD=∠ECA,于是可判断△CAD∽△CEA,利用相似三角形的性质得∠CAD=∠3,接着根据三角形外角性质有∠1=∠CAD+∠2=∠2+∠3,然后根据正方形得性质即可得到∠1+∠2+∠3=90°.
解答 解:设正方形的边长为1,则AC=$\sqrt{2}$,CD=1,CE=2,
∵$\frac{CD}{AC}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,$\frac{AC}{CE}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{CD}{AC}$=$\frac{AC}{CE}$,
而∠ACD=∠ECA,
∴△CAD∽△CEA,
∴∠CAD=∠3,
∵∠1=∠CAD+∠2,
∴∠1=∠2+∠3,
∵∠1=45°,
∴∠1+∠2+∠3=2∠1=90°.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.也考查了正方形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知α为锐角,则m=sin2α+cos2α的值( )
| A. | m>1 | B. | m=1 | C. | m<1 | D. | m≥1 |
14.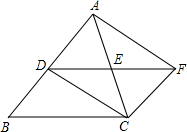 如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
 如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 任意四边形 |
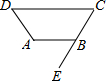 如图,AB∥CD,∠ABE=50°,∠D=∠C,则∠D=50°.
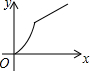
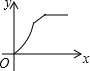
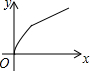
如图,AB∥CD,∠ABE=50°,∠D=∠C,则∠D=50°.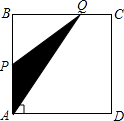 如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )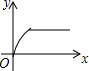
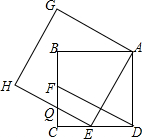 如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.
如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.