题目内容
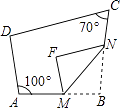
【题目】如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC= ![]() ,则四边形MABN的面积是( )
,则四边形MABN的面积是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】连接CD,交MN于E,
∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,
∴MN⊥CD,且CE=DE,
∴CD=2CE,
∵MN∥AB,
∴CD⊥AB,
∴△CMN∽△CAB,
∴ ![]() ,
,
∵在△CMN中,∠C=90°,MC=6,NC= ![]() ,
,
∴ ![]() =
= ![]() CMCN=
CMCN= ![]() ×6×
×6× ![]() =
= ![]() ,
,
∴ ![]() =4
=4 ![]() =4×
=4× ![]() =
= ![]() ,
,
∴S四边形MABN= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() .
.
答案为:C
由MN∥AB ,可得△CMN∽△CAB,再由相似三角形的性质,面积比等于其相似比的平方,先求出S Δ C M N , 再S Δ C A B ﹣ S Δ C M N,可求出四边形MABN的面积.

练习册系列答案
相关题目