题目内容
1.计算2sin45°-$\sqrt{3}tan30°+cos60°$+|$\frac{3}{2}$|=$\sqrt{2}$+1.分析 原式利用特殊角的三角函数值,以及绝对值的代数意义化简,计算即可得到结果.
解答 解:原式=2×$\frac{\sqrt{2}}{2}$-$\sqrt{3}$×$\frac{\sqrt{3}}{3}$+$\frac{1}{2}$+$\frac{3}{2}$=$\sqrt{2}$-1+2=$\sqrt{2}$+1,
故答案为:$\sqrt{2}$+1
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.如果□×3(ab)2=9a3b2,则□内应填的代数式是( )
| A. | ab | B. | 3ab | C. | a | D. | 3a |
5.下列计算正确的是( )
| A. | a8÷a2=a4 | B. | a3•a2=a6 | C. | (-2a3)2=4a9 | D. | 6x2•3xy=18x3y |
8.下列说法正确的是( )
| A. | 0的立方根是0.2 | B. | 4的平方根是±4 | C. | -1的立方根是-1 | D. | -25没有立方根 |
9.用加减消元法解方程组$\left\{\begin{array}{l}{3x-2y=1}\\{3x+y=3}\end{array}\right.$,正确消元后可得方程( )
| A. | 6x-y=4 | B. | 3y=2 | C. | -3y=2 | D. | -y=2 |
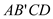 沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,
沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,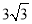 ,OD=
,OD=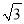 ,求CD的长
,求CD的长