题目内容
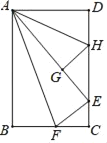
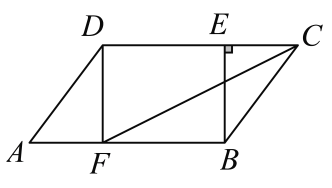
【题目】在![]() ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BE=4,求CD的长.
【答案】(1)详见解析;(2)8
【解析】
(1)先求出四边形BFDE是平行四边形,再根据矩形的判定推出即可;
(2)根据勾股定理求出BC长,求出CB=BF,即可得出答案.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵AF=CE,
∴FB=ED.
∴四边形DFBE是平行四边形.
∵BE⊥CD,
∴∠BED=90°.
∴四边形DFBE是矩形.
(2)在Rt△BEC中, BE=4, CE=3,
∴CB=5.
∵CF平分∠BCD,
∴∠DCF=∠BCF.
∵AB∥CD,
∴∠DCF=∠CFB.
∴∠BCF=∠CFB.
∴CB=BF=5.
∴CD= 8 .

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?