题目内容
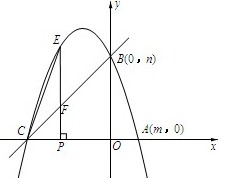
已知一元二次方程x2-4x+3=0的两根是m,n且m<n,如图所示,若抛物线y=-x2+bx +c的图像经过点A(m,0)、B(0,n);
(1) 求抛物线的解析式;
(2) 若(1)中的抛物线与x轴的另一个交点为C,根据图像回答,当x取何值时,抛物线的图像在直线BC的上方?
(3) 点P在线段OC上,作PE⊥x轴与抛物线交与点E,若直线BC将△CPE的面积分成相等的两部分,求点P的坐标。
(1) 求抛物线的解析式;
(2) 若(1)中的抛物线与x轴的另一个交点为C,根据图像回答,当x取何值时,抛物线的图像在直线BC的上方?
(3) 点P在线段OC上,作PE⊥x轴与抛物线交与点E,若直线BC将△CPE的面积分成相等的两部分,求点P的坐标。

| 解:(1)∵x2-4x+3=0的两个根为x1=1,x2=3, ∴A点的坐标为(1,0),B点的坐标为(0,3), 又∵抛物线y=-x2+bx+c的图像经过点A(1,0)、B(0,3)两点, ∴ 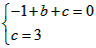 得 得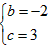 ∴抛物线的解析式为y=-x2-2x+3; |
|
|
(2)作直线BC, |
 |
| (3)设直线BC交PE于F,P点坐标为(a,0), 则E点坐标为(a,-a2-2a+3) ∵直线BC将△CPE的面积分成相等的两部分 ∴F是线段PE的中点. 即F点的坐标是(a, 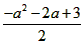 ) ) ∵直线BC过点B(0,3)和C(-3,0) 易得直线BC的解析式为y=x+3 ∵点F在直线BC上,所以点F的坐标满足直线BC的解析式 即 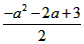 =a+3 =a+3解得a1=-1,a2=-3(此时P点与点C重合,舍去) ∴P点的坐标是(-1,0)。 |

练习册系列答案
相关题目