题目内容
已知a、b、c是△ABC的三边,且满足|a-5|+(b-4)2=0,则第三边c的取值范围是 .
考点:三角形三边关系,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:首先根据非负数的性质可得a-5=0,b-4=0,计算出a、b的值,然后再根据三角形的三边关系定理可得c的取值范围.
解答:解:∵|a-5|+(b-4)2=0,
∴a-5=0,b-4=0,
解得:a=5,b=4,
∵a、b、c是△ABC的三边,
∴5-4<c<5+4,
∴1<c<9.
故答案为:1<c<9.
∴a-5=0,b-4=0,
解得:a=5,b=4,
∵a、b、c是△ABC的三边,
∴5-4<c<5+4,
∴1<c<9.
故答案为:1<c<9.
点评:此题主要考查了非负数的性质,以及三角形三边关系定理,关键是掌握三角形两边之和大于第三边,三角形的两边差小于第三边.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
已知(m+2)x|m|-1+3=0为一元二次方程式,则m的值为( )
| A、2 | B、-2 |
| C、2或-2 | D、以上都不对 |
 如图,Rt△ABC中,∠ACB=90°,CD丄AB于D.
如图,Rt△ABC中,∠ACB=90°,CD丄AB于D.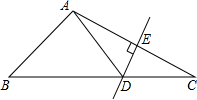 如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是
如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是
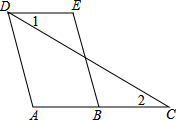 如图,AD∥BE,∠1=∠2,∠A=105°,求∠E的度数.
如图,AD∥BE,∠1=∠2,∠A=105°,求∠E的度数. 如图,∠1=∠2=35°,则AB∥CD,理由是
如图,∠1=∠2=35°,则AB∥CD,理由是 二次函数y=-2x2+4x的对称轴是x=
二次函数y=-2x2+4x的对称轴是x=