题目内容
6.已知矩形ABCD中,AB=2,BC=4,经过对角线AC中点O的直线垂直于AC,分别交BC于E,交AD于F,求EF的长及四边形AECF的面积.分析 由矩形的性质得出∠B=90°,AD∥BC,由ASA证明△AOF≌△COE,得出OF=OE,得出四边形AECF是平行四边形,由EF⊥AC得出四边形AECF是菱形,得出AE=CE,设AE=CE=x,则BE=4-x,由勾股定理得出方程,解方程求出AE,再由勾股定理求出AC,得出OA=$\sqrt{5}$,由勾股定理求出OE,即可得出EF的长,四边形AECF的面积=$\frac{1}{2}$AC•EF,即可得出结果.
解答 解:如图所示: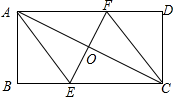
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠OAF=∠OCE,
∵O是AC的中点,
∴OA=OC,
在△AOF和△COE中,
$\left\{\begin{array}{l}{∠OAF=∠OCE}&{\;}\\{OA=OC}&{\;}\\{∠AOF=∠COE}&{\;}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴OF=OE,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形,
∴AE=CE,
设AE=CE=x,则BE=4-x,
由勾股定理得:AB2+BE2=AE2,
即22+(4-x)2=x2,
解得:x=$\frac{5}{2}$,
∴AE=$\frac{5}{2}$,
∵AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴OA=$\sqrt{5}$,
∴OE=$\sqrt{A{E}^{2}-O{A}^{2}}$=$\sqrt{(\frac{5}{2})^{2}-(\sqrt{5})^{2}}$=$\frac{\sqrt{5}}{2}$,
∴EF=2OE=$\sqrt{5}$,
∴四边形AECF的面积=$\frac{1}{2}$AC•EF=$\frac{1}{2}$×2$\sqrt{5}$×$\sqrt{5}$=5.
点评 本题考查了矩形的性质、菱形的判定与性质、全等三角形的判定与性质、勾股定理、平行四边形的判定等知识;本题综合性强,有一定难度.

| A. | x轴上方(含x轴) | B. | x轴下方(含x轴) | C. | y轴右方(含y轴) | D. | y轴左方(含y轴) |
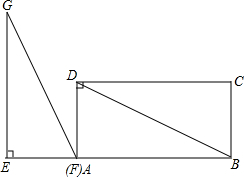 如图,在矩形ABCD中,DB=6,AD=3,在Rt△EFG中,∠GEF=90°,EF=3,GF=6,△EFG(点F和点A重合)的边EF和矩形的边AB在同一直线上.现Rt△EFG将从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,解答下列问题:
如图,在矩形ABCD中,DB=6,AD=3,在Rt△EFG中,∠GEF=90°,EF=3,GF=6,△EFG(点F和点A重合)的边EF和矩形的边AB在同一直线上.现Rt△EFG将从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,解答下列问题: 如图,已知点O是平行四边形ABCD的对角线AC的中点,四边形OCDE是平行四边形,求证:OE与AD平分.
如图,已知点O是平行四边形ABCD的对角线AC的中点,四边形OCDE是平行四边形,求证:OE与AD平分. 清晨,小强沿着一个如图所示的六边形广场周围的小路,按顺时针方向跑步
清晨,小强沿着一个如图所示的六边形广场周围的小路,按顺时针方向跑步 如图,O是直线AB上一点,OC平分∠AOB,∠COD=31°28′,则∠BOD的度数为58°32′.
如图,O是直线AB上一点,OC平分∠AOB,∠COD=31°28′,则∠BOD的度数为58°32′.