题目内容
 如图,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,则△ABC与△AEG的面积之间的关系为( )
如图,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,则△ABC与△AEG的面积之间的关系为( )| A、S△ABC≥S△AEG |
| B、S△ABC≤S△AEG |
| C、S△ABC=S△AEG |
| D、无法确定 |
考点:全等三角形的判定与性质,正方形的性质
专题:
分析:过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,则∠AMC=∠ANG=90°,根据正方形性质得出∠BAE=∠CAG=90°,AB=AE,AC=AG,求出∠NAG=∠MAC,证△ACM≌△AGN(,推出CM=GN,根据三角形的面积公式求出即可.
解答:解:△ABC与△AEG面积相等,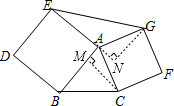 理由是:
理由是:
过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,则∠AMC=∠ANG=90°,
∵四边形ABDE和四边形ACFG都是正方形,
∴∠BAE=∠CAG=90°,AB=AE,AC=AG,
∵∠BAE+∠CAG+∠BAC+∠EAG=360°,
∴∠BAC+∠EAG=180°,
∵∠EAG+∠GAN=180°,
∴∠BAC=∠GAN,
在△ACM和△AGN中,
,
∴△ACM≌△AGN(AAS),
∴CM=GN,
∵S△ABC=
AB•CM,S△AEG=
AE•GN,
∴S△ABC=S△AEG.
故选C.
 理由是:
理由是:过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,则∠AMC=∠ANG=90°,
∵四边形ABDE和四边形ACFG都是正方形,
∴∠BAE=∠CAG=90°,AB=AE,AC=AG,
∵∠BAE+∠CAG+∠BAC+∠EAG=360°,
∴∠BAC+∠EAG=180°,
∵∠EAG+∠GAN=180°,
∴∠BAC=∠GAN,
在△ACM和△AGN中,
|
∴△ACM≌△AGN(AAS),
∴CM=GN,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=S△AEG.
故选C.
点评:本题考查了正方形的性质,全等三角形的性质和判定,三角形的面积等知识点的应用,关键是作辅助线后求出CM=GN.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知实数a,b,c,并且
=
=
=k,则直线y=kx-3一定通过( )
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| A、第一、二、三象限 |
| B、第三、四象限 |
| C、第一、三、四象限 |
| D、第一、二象限 |
若a2=25,b2=36,且ab<0,则a-b的值为( )
| A、-1或11 | B、-1或-11 |
| C、±1 | D、±11 |
下列计算中,错误的是( )
| A、a2+a2=2a2 |
| B、a2+a4=a6 |
| C、a6÷a2=a4 |
| D、(ab3)2=a2b6 |
