题目内容
如图，△OAB，△ACD是等边三角形，点A、C在x轴上，点B、D在函数
（x＞0）的图象上，则△ACD与△OAB的边长之比为（ ）
A．
B．
C．
D．
【答案】分析：设△OAB，△ACD边长的一半为a，b，根据等边三角形的性质可得点B的纵坐标，点D的纵坐标，代入反比例函数解析式可得两个等边三角形边长的一半，即可求出△ACD与△OAB的边长之比．
解答：
解：如图，分别过点B，D作x轴的垂线，垂足分别为E，F．设OE=a，AF=b，则BE=
a，DF=
b，
∴点B，D的坐标为（a，
a），（2a+b，
b），
∵点B、D在函数
（x＞0）的图象上，
∴a×
a=（2a+b）×
b=
，
解得a=1，b=
-1．
∴△ACD与△OAB的边长之比=2b：2a=b：a=
-1．
故选A．
点评：本题综合考查了等边三角形和反比例函数的性质；得到用等边三角形边长的一半表示点B和点D的坐标是解决本题的突破点．
解答：
解：如图，分别过点B，D作x轴的垂线，垂足分别为E，F．设OE=a，AF=b，则BE=a，DF=b，∴点B，D的坐标为（a，
a），（2a+b，b），∵点B、D在函数
（x＞0）的图象上，∴a×
a=（2a+b）×b=，解得a=1，b=
-1．∴△ACD与△OAB的边长之比=2b：2a=b：a=
-1．故选A．
点评：本题综合考查了等边三角形和反比例函数的性质；得到用等边三角形边长的一半表示点B和点D的坐标是解决本题的突破点．
练习册系列答案
相关题目
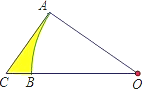如图，OAB是以6cm为半径的扇形，AC切弧AB于点A交OB的延长线于点C，如果弧AB的长等于3cm，AC=4cm，则图中阴影部分的面积为（ ）| A、15cm2 | B、6cm2 | C、4cm2 | D、3cm2 |
6、如图，△OAB和△OCD是位似图形，则位似中心是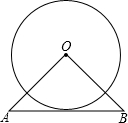
如图，△OAB是等腰直角三角形，∠AOB=90°，AB=8，且AB与⊙O相切，则⊙O的半径为
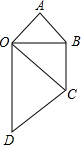如图，△OAB是等腰直角三角形，∠A=90°，AO=AB．以斜边OB为直角边，按顺时针方向画等腰直角三角形OBC，再以同样的方法画等腰直角三角形OCD．