题目内容
通过观察a2+b2-2ab=(a-b)2≥0可知: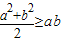 ,与此类比,当a≥0,b≥0时,
,与此类比,当a≥0,b≥0时, ______
______
【答案】分析:由( )2+(
)2+( )2-2
)2-2 =(
=( -
- )2≥0,即可得
)2≥0,即可得 ≥
≥ ;
;
(1)由 ≥
≥ ,可得a+b≥2
,可得a+b≥2 ,则可得x+
,则可得x+ ≥2
≥2 =2,继而证得结论;
=2,继而证得结论;
(2)首先将x+ 变形为(x-1)+
变形为(x-1)+ +1,然后利用几何不等式,即可证得结论;
+1,然后利用几何不等式,即可证得结论;
(3)首先将2x2+ 变形为2(x2+1)+
变形为2(x2+1)+ -2,然后利用几何不等式求解,即可求得最小值.
-2,然后利用几何不等式求解,即可求得最小值.
解答:解:∵( )2+(
)2+( )2-2
)2-2 =(
=( -
- )2≥0,
)2≥0,
即a+b-2 ≥0,
≥0,
∴ ≥
≥ ;
;
(1)证明:∵x>0,
∴x+ ≥2
≥2 =2,
=2,
即x+ ≥2;
≥2;
(2)证明:∵x>1,
∴x+ =(x-1)+
=(x-1)+ +1≥2
+1≥2 +1=2+1=3,
+1=2+1=3,
即x+ ≥3;
≥3;
(3)解:2x2+ =2(x2+1)+
=2(x2+1)+ -2≥2
-2≥2 -2=2
-2=2 -2,
-2,
∴2x2+ 的最小值为2
的最小值为2 -2.
-2.
故答案为: ,(4)2
,(4)2 -2.
-2.
点评:此题考查了几何不等式的证明与应用.此题难度适中,解题的关键是掌握几何不等式的应用.
 )2+(
)2+( )2-2
)2-2 =(
=( -
- )2≥0,即可得
)2≥0,即可得 ≥
≥ ;
;(1)由
 ≥
≥ ,可得a+b≥2
,可得a+b≥2 ,则可得x+
,则可得x+ ≥2
≥2 =2,继而证得结论;
=2,继而证得结论;(2)首先将x+
 变形为(x-1)+
变形为(x-1)+ +1,然后利用几何不等式,即可证得结论;
+1,然后利用几何不等式,即可证得结论;(3)首先将2x2+
 变形为2(x2+1)+
变形为2(x2+1)+ -2,然后利用几何不等式求解,即可求得最小值.
-2,然后利用几何不等式求解,即可求得最小值.解答:解:∵(
 )2+(
)2+( )2-2
)2-2 =(
=( -
- )2≥0,
)2≥0,即a+b-2
 ≥0,
≥0,∴
 ≥
≥ ;
;(1)证明:∵x>0,
∴x+
 ≥2
≥2 =2,
=2,即x+
 ≥2;
≥2;(2)证明:∵x>1,
∴x+
 =(x-1)+
=(x-1)+ +1≥2
+1≥2 +1=2+1=3,
+1=2+1=3,即x+
 ≥3;
≥3;(3)解:2x2+
 =2(x2+1)+
=2(x2+1)+ -2≥2
-2≥2 -2=2
-2=2 -2,
-2,∴2x2+
 的最小值为2
的最小值为2 -2.
-2.故答案为:
 ,(4)2
,(4)2 -2.
-2.点评:此题考查了几何不等式的证明与应用.此题难度适中,解题的关键是掌握几何不等式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
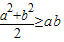 ,与此类比,当a≥0,b≥0时,
,与此类比,当a≥0,b≥0时,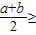 ______
______