题目内容
通过观察a2+b2-2ab=(a-b)2≥0可知:
≥ab,与此类比,当a≥0,b≥0时,
≥______(要求填写),你观察得到的这个不等式是一个重要不等式,它在证明不等式和求函数的极大值或者极小值中非常有用.请你运用上述不等式解决下列问题:
(1)求证:当x>0时,x+
≥2;
(2)求证:当x>1时,x+
≥3;
(3)2x2+
的最小值是______.
| a2+b2 |
| 2 |
| a+b |
| 2 |
(1)求证:当x>0时,x+
| 1 |
| x |
(2)求证:当x>1时,x+
| 1 |
| x-1 |
(3)2x2+
| 1 |
| x2+1 |
∵(
)2+(
)2-2
=(
-
)2≥0,
即a+b-2
≥0,
∴
≥
;
(1)证明:∵x>0,
∴x+
≥2
=2,
即x+
≥2;
(2)证明:∵x>1,
∴x+
=(x-1)+
+1≥2
+1=2+1=3,
即x+
≥3;
(3)2x2+
=2(x2+1)+
-2≥2
-2=2
-2,
∴2x2+
的最小值为2
-2.
故答案为:
,(4)2
-2.
| a |
| b |
| ab |
| a |
| b |
即a+b-2
| ab |
∴
| a+b |
| 2 |
| ab |
(1)证明:∵x>0,
∴x+
| 1 |
| x |
x•
|
即x+
| 1 |
| x |
(2)证明:∵x>1,
∴x+
| 1 |
| x-1 |
| 1 |
| x-1 |
(x-1)•
|
即x+
| 1 |
| x-1 |
(3)2x2+
| 1 |
| x2+1 |
| 1 |
| x2+1 |
2(x2+1)•
|
| 2 |
∴2x2+
| 1 |
| x2+1 |
| 2 |
故答案为:
| ab |
| 2 |

练习册系列答案
相关题目
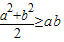 ,与此类比,当a≥0,b≥0时,
,与此类比,当a≥0,b≥0时,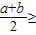 ______
______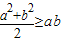 ,与此类比,当a≥0,b≥0时,
,与此类比,当a≥0,b≥0时, ______
______