Question

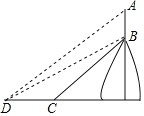
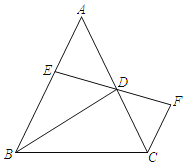
【题目】已知：如图，在△ABC中AB＝AC，BD平分∠ABC交AC于点D，DE平分∠ADB交AB于点E，CF∥AB交ED的延长线于F，若∠A＝52°，求∠DFC的度数．

Answer 1

【答案】80°

【解析】

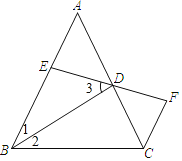
根据三角形的内角和以及等腰三角形的性质可得到∠ABC＝∠ACB＝64°，根据角平分线的定义得到∠1＝∠2＝∠ABC＝32°，再根据三角形外角的性质可得出∠ADB的度数，从而可得出∠3的度数，可进一步得出∠AEF的度数，最后根据平行线的性质即可得到结论．

解：∵∠A＝52°，∠A+∠ABC+∠ACB＝180°，∴∠ABC+∠ACB＝128°，

∵AB＝AC，

∴∠ABC＝∠ACB＝64°，

∵BD平分∠ABC，

∴∠1＝∠2＝∠ABC＝32°，

∴∠ADB＝∠ACB+∠2＝64°+32°＝96°，

∵DE平分∠ADB，

∴∠3＝∠ADB＝48°，

∴∠AEF＝∠1+∠3＝32°+48°＝80°，

∵CF∥AB，

∴∠DFC＝∠AEF＝80°．