题目内容
(1)3(x-5)2=2(5-x)
(2)(3x-1)2=49
(3)2x2-7x+3=0
(4)(x-1)(x+2)=4.
(2)(3x-1)2=49
(3)2x2-7x+3=0
(4)(x-1)(x+2)=4.
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法
专题:计算题
分析:(1)方程移项分解后,利用因式分解法求出解即可;
(2)方程利用平方根定义开方即可求出解;
(3)方程左边分解因式后,利用因式分解法求出解即可;
(4)方程整理后,利用因式分解法求出解即可.
(2)方程利用平方根定义开方即可求出解;
(3)方程左边分解因式后,利用因式分解法求出解即可;
(4)方程整理后,利用因式分解法求出解即可.
解答:解:(1)方程变形得:3(xx-5)2+(x-5)=0,
分解因式得:(3x-15+1)(x-5)=0,
解得:x1=
,x2=5;
(2)开方得:3x-1=7或3x-1=-7,
解得:x1=
,x2=-2;
(3)分解得:(2x-1)(x-3)=0,
可得2x-1=0或x-3=0,
解得:x1=
,x2=3;
(4)方程整理得:x2+x-6=0,
分解得:(x-2)(x+3)=0,
可得x-2=0或x+3=0,
解得:x1=2,x2=-3.
分解因式得:(3x-15+1)(x-5)=0,
解得:x1=
| 14 |
| 3 |
(2)开方得:3x-1=7或3x-1=-7,
解得:x1=
| 8 |
| 3 |
(3)分解得:(2x-1)(x-3)=0,
可得2x-1=0或x-3=0,
解得:x1=
| 1 |
| 2 |
(4)方程整理得:x2+x-6=0,
分解得:(x-2)(x+3)=0,
可得x-2=0或x+3=0,
解得:x1=2,x2=-3.
点评:此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
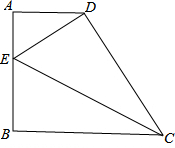 在直角梯形ABCD中,∠A=∠B=90°,AD=3,BC=6,AB=m(m>3),ED⊥CD且交AB于点E,
在直角梯形ABCD中,∠A=∠B=90°,AD=3,BC=6,AB=m(m>3),ED⊥CD且交AB于点E,