题目内容
 如图,∠A是⊙O的圆周角,∠A=40°,则∠OBC=
如图,∠A是⊙O的圆周角,∠A=40°,则∠OBC=
- A.30°
- B.40°
- C.50°
- D.60°
C
分析:根据一条弧所对的圆周角等于它所对的圆心角的一半求得∠BOC,再根据三角形的内角和定理以及等腰三角形的两个底角相等进行计算.
解答:根据圆周角定理,得
∠BOC=2∠A=80°
∵OB=OC
∴∠OBC=∠OCB= =50°.
=50°.
故选C.
点评:综合运用了圆周角定理、等腰三角形的性质和三角形的内角和定理.
分析:根据一条弧所对的圆周角等于它所对的圆心角的一半求得∠BOC,再根据三角形的内角和定理以及等腰三角形的两个底角相等进行计算.
解答:根据圆周角定理,得
∠BOC=2∠A=80°
∵OB=OC
∴∠OBC=∠OCB=
 =50°.
=50°.故选C.
点评:综合运用了圆周角定理、等腰三角形的性质和三角形的内角和定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1997•上海)如图,半径是5厘米的圆中,8厘米长的弦的弦心距是
(1997•上海)如图,半径是5厘米的圆中,8厘米长的弦的弦心距是
 如图,半径是5厘米的圆中,8厘米长的弦的弦心距是________厘米.
如图,半径是5厘米的圆中,8厘米长的弦的弦心距是________厘米.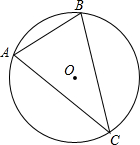 如图,⊙O是△ABC的________圆,△ABC是⊙O的________三角形.
如图,⊙O是△ABC的________圆,△ABC是⊙O的________三角形. 如图,半径是5厘米的圆中,8厘米长的弦的弦心距是 厘米.
如图,半径是5厘米的圆中,8厘米长的弦的弦心距是 厘米.