题目内容
如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D、E是BC边上的任意两点,且∠DAE=45°.
(1)将△ABD绕点A逆时针旋转90°,得到△ACF,请在图(1)中画出△ACF.
(2)在(1)中,连接EF,探究线段BD,EC和DE之间有怎样的数量关系?写出猜想,并说明理由.
(3)如图2,M、N分别是正方形ABCD的边BC、CD上一点,且BM+DN=MN,试求∠MAN的大小.

(1)将△ABD绕点A逆时针旋转90°,得到△ACF,请在图(1)中画出△ACF.
(2)在(1)中,连接EF,探究线段BD,EC和DE之间有怎样的数量关系?写出猜想,并说明理由.
(3)如图2,M、N分别是正方形ABCD的边BC、CD上一点,且BM+DN=MN,试求∠MAN的大小.

考点:全等三角形的判定与性质,勾股定理,旋转的性质
专题:
分析:(1)完成图形;
(2)易证∠DAE=∠FAE=45°,即可证明△DAE≌△FAE,可得EF=DE,根据∠ACF=45°可证∠ECF=90°,根据勾股定理可得EF2=EC2+FC2,即可解题;
(3)由旋转得:∠NAE=90°,AN=AE,∠ABE=∠D=90°,可得ME=MN,即可证明△AEM≌△ANM,可得∠MAE=∠MAN=45°,即可解题.
(2)易证∠DAE=∠FAE=45°,即可证明△DAE≌△FAE,可得EF=DE,根据∠ACF=45°可证∠ECF=90°,根据勾股定理可得EF2=EC2+FC2,即可解题;
(3)由旋转得:∠NAE=90°,AN=AE,∠ABE=∠D=90°,可得ME=MN,即可证明△AEM≌△ANM,可得∠MAE=∠MAN=45°,即可解题.
解答:解:(1)完成图形,

(2)连接EF,

由旋转可知,AF=AD,CF=BD,∠DAF=90°,
∵∠DAE=45°,
∴∠DAE=∠FAE=45°,
在△DAE和△FAE中,
,
∴△DAE≌△FAE(SAS),
∴EF=DE,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠ACF=45°,
∴∠ECF=∠ACB+∠ACF=90°,
∴EF2=EC2+FC2,
∴DE2=EC2+BD2;
(3)将△ADN绕点A逆时针旋转,得到△ABE,如图:

由旋转得:∠NAE=90°,AN=AE,∠ABE=∠D=90°,
∴E,B,M三点共线,
∵BM+DN=MN,
∴ME=MN,
在△AEM和△ANM中,
,
∴△AEM≌△ANM(SSS),
∴∠MAE=∠MAN=45°.

(2)连接EF,

由旋转可知,AF=AD,CF=BD,∠DAF=90°,
∵∠DAE=45°,
∴∠DAE=∠FAE=45°,
在△DAE和△FAE中,
|
∴△DAE≌△FAE(SAS),
∴EF=DE,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠ACF=45°,
∴∠ECF=∠ACB+∠ACF=90°,
∴EF2=EC2+FC2,
∴DE2=EC2+BD2;
(3)将△ADN绕点A逆时针旋转,得到△ABE,如图:

由旋转得:∠NAE=90°,AN=AE,∠ABE=∠D=90°,
∴E,B,M三点共线,
∵BM+DN=MN,
∴ME=MN,
在△AEM和△ANM中,
|
∴△AEM≌△ANM(SSS),
∴∠MAE=∠MAN=45°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△DAE≌△FAE和△AEM≌△ANM是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
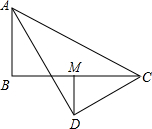 在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC.
在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC. 如图,兴华中学有两块紧挨着的边长分别为a,b的正方形空地,为了美化校园,现打算在图中阴影部分种植草皮,求所要种植草皮的面积.
如图,兴华中学有两块紧挨着的边长分别为a,b的正方形空地,为了美化校园,现打算在图中阴影部分种植草皮,求所要种植草皮的面积.