题目内容
10．
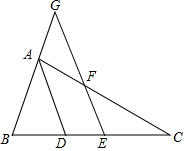如图，△ABC中，AD平分∠BAC，EF交BA延长线于点G，∠CFE=∠G．（1）求证：AD∥EG；
（2）设∠B=x，∠G=y，若x-y=30°，∠ADC=110°，求∠B的度数．
分析 （1）由角平分线得∠BAC=2∠2，由∠3=∠G=∠4知∠BAC=2∠4，即可得∠2=∠4，从而得证；
（2）由外角性质得∠ADC=∠B+∠1=110°，即x+y=110°，结合已知条件解方程组即可得．
解答 解：（1）如图，
∵AD平分∠BAC，
∴∠1=∠2，
∵∠3=∠G，∠3=∠4，
∴∠4=∠G，
∵∠BAC=2∠3=∠G+∠4，
∴2∠2=∠4+∠4，
∴∠2=∠4，
∴AD∥EG；
（2）∵∠ADC=∠B+∠1=110°，
∴$\left\{\begin{array}{l}{x+y=110°}\\{x-y=30°}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=70°}\\{y=40°}\end{array}\right.$，
∴∠B=70°
点评 本题主要考查角平分线、平行线的判定及三角形外角性质，熟练掌握角平分线的性质和三角形外角性质是解题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
2．今年我市有近5万名考生参加中考，为了解这些考生的数学成绩，从中抽取1000名考生的数学成绩进行统计分析，以下说法正确的是（ ）
| A． | 这1000名考生是总体的一个样本 | B． | 近5万名考生是总体 | ||
| C． | 每位考生的数学成绩是个体 | D． | 1000名学生的数学成绩是样本容量 |
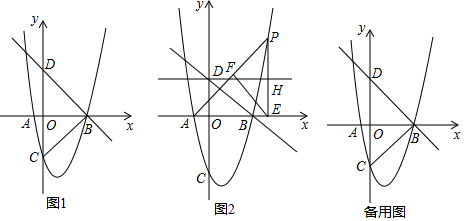
5．在平面直角坐标系中，将抛物线C1：y=x2平移后得到抛物线C2，使得抛物线C2恰好经过抛物线C1的顶点，且抛物线C2与x轴有两个交点，分别记为点A、点B．若AB=2$\sqrt{3}$，抛物线C2的顶点为点C，则△ABC的周长是（ ）
| A． | 3+2$\sqrt{2}$ | B． | 6+2$\sqrt{3}$ | C． | 6$\sqrt{3}$ | D． | 12$\sqrt{3}$ |
如图，在平面直角坐标系中，ABC的三个顶点坐标为A（-3，4），B（-4，2），C（-2，1），△ABC绕原点顺时针旋转90°，得到△A1B1C1，△A1B1C1向左平移2个单位，再向下平移5个单位得到△A2B2C2．