题目内容
7.设m,n是方程x2-x-2013=0的两个实数根.则m2+n的值为2014.分析 先根据根与系数的关系可求m+n的值,再求出m=1-n,根据m是方程x2-x-2013=0的实数根得:m2-m-2013=0,把m=1-n代入可得结论.
解答 解:∵m,n是方程x2-x-2013=0的两个实数根,
∴m+n=1,
∴m=1-n,
∵m是方程x2-x-2013=0的实数根.
∴m2-m-2013=0,
m2-(1-n)=2013,
m2+n=2014.
故答案为:2014.
点评 本题考查了根与系数的关系,解题的关键是利用根与系数关系和方程根的定义相结合进行变形.

练习册系列答案
相关题目
15.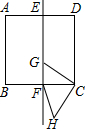 如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )
如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )
 如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )
如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )| A. | $\frac{1}{2}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3 |
2.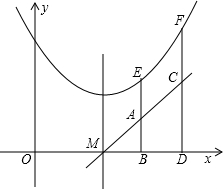 如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
 如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )| A. | S=y2+y1 | B. | S=y2+2y1 | C. | S=y2-y1 | D. | S=y2-2y1 |
12.已知x=-1,y=2是二元一次方程组3x+2y=m,nx-y=1的解,则m-n的值是( )
| A. | 0 | B. | -2 | C. | 1 | D. | 4 |
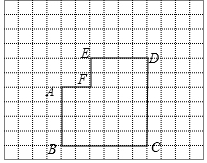 下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.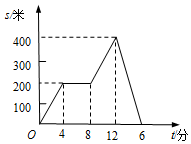 小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.
小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.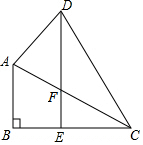 如图,在四边形ABCD中,∠B=90°,过点D作DE∥AB,交BC于E,且DE=BC,连接AC交AC于F,若∠ACB=∠CDE=30°,则图中有几个等腰三角形?请找出来并说明理由.
如图,在四边形ABCD中,∠B=90°,过点D作DE∥AB,交BC于E,且DE=BC,连接AC交AC于F,若∠ACB=∠CDE=30°,则图中有几个等腰三角形?请找出来并说明理由.