题目内容
13. 吉福市实行了生活用电按三个档次收费方案,下图是每户人家每月用电费y(元)与用电量x(度)间的关系
吉福市实行了生活用电按三个档次收费方案,下图是每户人家每月用电费y(元)与用电量x(度)间的关系(1)根据图中折线,电费收据方案分为三个档次,填写下表:
(2)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(3)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度缴纳电费153元,求m值.
| 档次 | 第一档 | 第二档 | 第三档 |
| 每月用电量x度 | 0<x≤140 | 140<x≤ 230 | x> 230 |
分析 (1)根据折线统计图中的横坐标,可得答案
(2)根据待定系数法,可得函数关系式;
(3)根据待定系数法,可得第二档的函数解析式,第三档的函数解析式,根据有理数的减法,可得答案.
解答 解:(1)观察折线统计图,得
| 档次 | 第一档 | 第二档 | 第三档 |
| 每月用电量x度 | 0<x≤140 | 140<x≤ 230 | x> 230 |
$\left\{\begin{array}{l}{140{k}_{1}+{b}_{1}=63}\\{230{k}_{1}+{b}_{1}=108}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=\frac{1}{2}}\\{{b}_{1}=-7}\end{array}\right.$.
第二档的函数解析式为y=$\frac{1}{2}$x-7;
(3)设第三档的函数解析式为y=k2x+b2,将(230,108),(290,153)代入函数解析式,得
$\left\{\begin{array}{l}{230{k}_{2}+{b}_{2}=108}\\{290{k}_{2}+{b}_{2}=153}\end{array}\right.$.解得$\left\{\begin{array}{l}{{k}_{2}=\frac{3}{4}}\\{{b}_{2}=-\frac{129}{2}}\end{array}\right.$.
第三档的函数解析式为y=$\frac{3}{4}$x-$\frac{129}{2}$,
m=k2-k1=$\frac{3}{4}$-$\frac{1}{2}$=$\frac{1}{4}$.
点评 本题考察了二次函数综合题,(1)观察函数图象的横坐标是解题关键;(2)利用了待定系数法求函数解析式;(3)利用k2-k1=m是解题关键.

练习册系列答案
相关题目
12.某校九年级学生中有女生226人,男生250人,计划组成甲、乙两种活动小组共40个,甲、乙两种活动小组每组的人数搭配情况如表:
设准备组成x个甲种活动小组,请解答下列问题:
(1)求x的值,并说明有哪几种符合题意的建立活动小组的方案;
(2)若甲种活动每组需要培训费50元,乙种活动每组需要培训费40元,说明(1)中哪种方案能节省经费,并计算最少经费为多少元.
| 需要女生 | 需要男生 | |
| 甲种活动 | 7人 | 4人 |
| 乙种活动 | 3人 | 10人 |
(1)求x的值,并说明有哪几种符合题意的建立活动小组的方案;
(2)若甲种活动每组需要培训费50元,乙种活动每组需要培训费40元,说明(1)中哪种方案能节省经费,并计算最少经费为多少元.
4.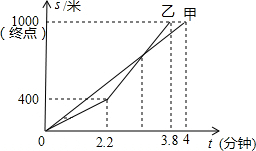 某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
 某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )| A. | 甲比乙先到达终点 | |
| B. | 甲比乙多走了200米 | |
| C. | 乙比甲少用了0.2分钟 | |
| D. | 比赛中两人从出发到2.2分钟时间段,乙的速度比甲的速度快 |
8. 如图所示为某几何体的示意图,该几何体的左视图应为( )
如图所示为某几何体的示意图,该几何体的左视图应为( )
 如图所示为某几何体的示意图,该几何体的左视图应为( )
如图所示为某几何体的示意图,该几何体的左视图应为( )| A. |  | B. |  | C. |  | D. |  |
18.tan30°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.下列运算正确的是( )
| A. | 2x+3y=5xy | B. | 5m2•m3=5m5 | C. | (a-b)2=a2-b2 | D. | (m2)3=m5 |
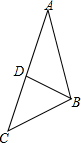 如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )
如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )