Question

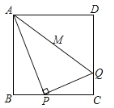
【题目】正方形ABCD的边长为4，P 为BC上的动点，连接PA，作PQ⊥PA，PQ交CD于Q，连接AQ ，则AQ的最小值是（ ）

A.5B.C.D.4

Answer 1

【答案】A

【解析】

设BP=x，CQ=y，根据△ABP∽△PCQ可得y关于x的二次函数，利用二次函数的性质，求得y的最大值情况，则QD最小，则AQ最小．

∵四边形ABCD是正方形，

∴∠B＝∠C＝90°，

∵PQ⊥AP，

∴∠APB+∠QPC＝90°，

∠APB+∠BAP＝90°，

∴∠BAP＝∠QPC，

∴△ABP∽△PCQ，

∴，

设BP=x，CQ=y

即，

∴y＝﹣+x＝﹣+1(0＜x＜4)，

∵﹣＜0，

∴y有最大值，

∴当x＝2时，y有最大值1cm．此时QD=3

在Rt△AQP中，

故AQ的最小值是5

故选：A．