题目内容
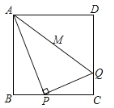
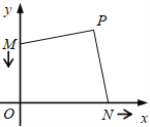
【题目】如图,动点![]() 从(0,3)出发,沿
从(0,3)出发,沿![]() 轴以每秒1个单位长度的速度向下移动,同时动点
轴以每秒1个单位长度的速度向下移动,同时动点![]() 从
从![]() 出发,沿
出发,沿![]() 轴以每秒2个单位长度的速度向右移动,当点
轴以每秒2个单位长度的速度向右移动,当点![]() 移动到
移动到![]() 点时,点
点时,点![]() 、
、![]() 同时停止移动.点
同时停止移动.点![]() 在第一象限内,在
在第一象限内,在![]() 、
、![]() 移动过程中,始终有
移动过程中,始终有![]() ,且
,且![]() .则在整个移动过程中,点
.则在整个移动过程中,点![]() 移动的路径长为( )
移动的路径长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由题意过P点作![]() 交于D点,作
交于D点,作![]() 交于E点,并利用全等三角形判定
交于E点,并利用全等三角形判定![]() ,得出
,得出![]() ,从而分当
,从而分当![]() 时,有
时,有![]() (0,3),
(0,3),![]()
![]() ,设P点坐标为
,设P点坐标为![]() 以及当
以及当![]() 时,有
时,有![]() 、O(0,0),
、O(0,0),![]() 、H
、H![]() ,设P点坐标为
,设P点坐标为![]() ,求出P点坐标,继而由点
,求出P点坐标,继而由点![]() 移动的路径为一条线段利用两点间距离公式求得点
移动的路径为一条线段利用两点间距离公式求得点![]() 移动的路径长.
移动的路径长.
解:由题意过P点作![]() 交于D点,作
交于D点,作![]() 交于E点,如图,
交于E点,如图,

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵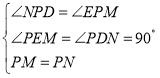 ,
,
∴![]() ,即有
,即有![]() ,
,
由题意可知![]() ,
,
当![]() 时,有
时,有![]() (0,3),
(0,3),![]()
![]() ,设P点坐标为
,设P点坐标为![]() ,
,
由![]() ,即有
,即有![]() ,解得
,解得![]() ,
,
即此时P点坐标为![]() ;
;
当![]() 时,有
时,有![]() 、O(0,0),
、O(0,0),![]() 、H
、H![]() ,设P点坐标为
,设P点坐标为![]() ,
,
由![]() 即图上
即图上![]() ,即有
,即有![]() ,
,
解得![]() ,即此时P点坐标为
,即此时P点坐标为![]() ;
;
由图可知点![]() 移动的路径为一条线段,
移动的路径为一条线段,
则点![]() 移动的路径长为:
移动的路径长为: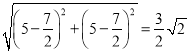 .
.
故选:A.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目