Question

【题目】在平面直角坐标系中，抛物线y＝﹣x2+bx+c经过点A、B，C，已知A（﹣1，0），C（0，3）．

（1）求抛物线的解析式；

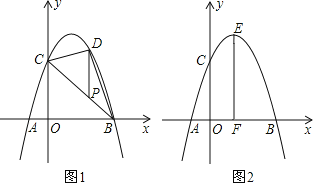
（2）如图1，P为线段BC上一动点，过点P作y轴的平行线，交抛物线于点D，是否存在这样的P点，使线段PD的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；

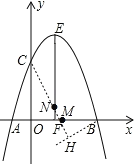
（3）如图2，抛物线的顶点为E，EF⊥x轴于点F，N是直线EF上一动点，M（m，0）是x轴一个动点，请直接写出CN+MN+MB的最小值以及此时点M、N的坐标，直接写出结果不必说明理由．

Answer 1

【答案】（1）y=﹣x2+2x+3；（2）存在，PD最大值为；（3），N（1，），M（，0）．

【解析】

（1）y=﹣x2+bx+c经过点C，则c=3，将点A的坐标代入抛物线表达式：y=﹣x2+bx+3，即可求解；

（2）设点D（x，﹣x2+2x+3），则点P（x，﹣x+3），则PD=（﹣x2+2x+3）﹣（﹣x+3）=﹣x2+3x，即可求解；

（3）过点B作倾斜角为30°的直线BH，过点C作CH⊥BH交于点H，CH交对称轴于点N，交x轴于点M，则点M、N为所求，即可求解．

（1）y=﹣x2+bx+c经过点C，则c=3，

将点A的坐标代入抛物线表达式：y=﹣x2+bx+3，得：0=-1-b+3，解得：b=2，

抛物线的表达式为：y=﹣x2+2x+3；

（2）存在，理由：

令y=0，得：﹣x2+2x+3=0，解得：x=﹣1或3，故点B（3，0），

设直线BC为y=kx+b，将点B、C的坐标代入得：

，解得：．

∴直线BC的表达式为：y=﹣x+3，

设点D（x，﹣x2+2x+3），则点P（x，﹣x+3），

则PD=（﹣x2+2x+3）﹣（﹣x+3）=﹣x2+3x=，

当x时，PD最大值为：；

（3）过点B作倾斜角为30°的直线BH，过点C作CH⊥BH交于点H，CH交对称轴于点N，交x轴于点M，则点M、N为所求．

∵∠ABH=30°，∠MHB=90°，∴∠CMO=∠BMH=90°-30°=60°．

∵∠COB=90°，∴∠COM=30°，∴OC=OM．

∵OC=3，∴OM=，

∴M（，0），CM=2OM=，MF=OM-OF=，MB=OB-OM=．

∵∠FMN=60°，∴tan∠FMN=，∴，

∴NF=，∴N（1，）．

CN+MNMB的最小值=CMMB=．