题目内容
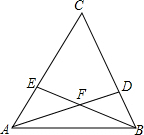 如图,△ABC中,AD,BE分别是△ABC中∠CAB,∠CBA的角平分线且交于F点.
如图,△ABC中,AD,BE分别是△ABC中∠CAB,∠CBA的角平分线且交于F点.(1)若∠C=60°,求∠AFB的大小;
(2)若∠AFB=α,则∠C是多少?
考点:三角形内角和定理
专题:
分析:(1)根据三角形的内角和定理和角平分线的定义求出∠ABF+∠BAF,再根据三角形的内角和定理列式计算即可得解;
(2)根据三角形的内角和定理求出∠ABF+∠BAF,根据角平分线的定义求出∠ABC+∠BAC,然后再利用三角形的内角和定理列式计算即可得解.
(2)根据三角形的内角和定理求出∠ABF+∠BAF,根据角平分线的定义求出∠ABC+∠BAC,然后再利用三角形的内角和定理列式计算即可得解.
解答:解:(1)∵∠C=60°,
∴∠ABC+∠BAC=180°-60°=120°,
∵AD,BE分别是∠CAB,∠CBA的角平分线,
∴∠ABF+∠BAF=
(∠ABC+∠BAC)=
×120°=60°,
在△ABF中,∠AFB=180°-(∠ABF+∠BAF)=180°-60°=120°;
(2)在△ABF中,∠ABF+∠BAF=180°-∠AFB=180°-α,
∵AD,BE分别是∠CAB,∠CBA的角平分线,
∴∠ABC+∠BAC=2(∠ABF+∠BAF)=360°-2α,
在△ABC中,∠C=180°-(∠ABC+∠BAC)=180°-(360°-2α)=2α-180°,
故∠C=2α-180°.
∴∠ABC+∠BAC=180°-60°=120°,
∵AD,BE分别是∠CAB,∠CBA的角平分线,
∴∠ABF+∠BAF=
| 1 |
| 2 |
| 1 |
| 2 |
在△ABF中,∠AFB=180°-(∠ABF+∠BAF)=180°-60°=120°;
(2)在△ABF中,∠ABF+∠BAF=180°-∠AFB=180°-α,
∵AD,BE分别是∠CAB,∠CBA的角平分线,
∴∠ABC+∠BAC=2(∠ABF+∠BAF)=360°-2α,
在△ABC中,∠C=180°-(∠ABC+∠BAC)=180°-(360°-2α)=2α-180°,
故∠C=2α-180°.
点评:本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠B的平分线与AD,AC交于E,F,
如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠B的平分线与AD,AC交于E,F,