题目内容
4.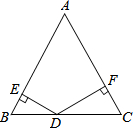 在等边△ABC中,AB=2cm,点D是BC边上的任意一点,DE⊥AB于点E,DF⊥AC于点F,BN⊥AC于点N,则DE+DF=$\sqrt{3}$ cm.
在等边△ABC中,AB=2cm,点D是BC边上的任意一点,DE⊥AB于点E,DF⊥AC于点F,BN⊥AC于点N,则DE+DF=$\sqrt{3}$ cm.
分析 作AG⊥BC于G,根据等边三角形的性质得出∠B=60°,解直角三角形求得AG=$\sqrt{3}$,根据S△ABD+S△ACD=S△ABC即可得出DE+DF=AG=$\sqrt{3}$cm.
解答 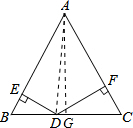 解:作AG⊥BC于G,
解:作AG⊥BC于G,
∵△ABC是等边三角形,
∴∠B=60°,
∴AG=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$cm,
连接AD,
∵S△ABD+S△ACD=S△ABC,
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$BC•AG,
∵AB=AC=BC=2,
∴DE+DF=AG=$\sqrt{3}$cm,
故答案为$\sqrt{3}$.
点评 本题考查了等边三角形的性质,解直角三角函数以及三角形面积等,根据S△ABD+S△ACD=S△ABC即可得出DE+DF=AG是解题的关键.

练习册系列答案
相关题目
16.若一元二次方程ax2+bx+c=0没有实数根,则二次函数y=ax2+bx+c的图象与x轴的交点有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
13.下列说法中不正确的是( )
| A. | 1.804精确到百分位是1.80 | |
| B. | 近似数3.14×104是精确到百分位 | |
| C. | 近似数5.0万是精确到千位 | |
| D. | 近似数1.8与1.80表示的意义不一样 |

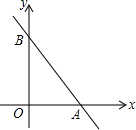 如图,直线y=-$\frac{4}{3}$x+4分别交x轴、y轴于A、B两点,现将线段AB绕点O顺时针旋转一周,则线段AB扫过的面积为$\frac{256}{25}π$.
如图,直线y=-$\frac{4}{3}$x+4分别交x轴、y轴于A、B两点,现将线段AB绕点O顺时针旋转一周,则线段AB扫过的面积为$\frac{256}{25}π$.