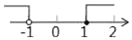��Ŀ����
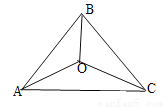
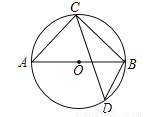
��ͼ����ABC������AB��BC��CA���ֱ���20��30��40����������ƽ���߽���ABC��Ϊ���������Σ���S��ABO�US��BCO�US��CAO ���� ��������
A. 1�U1�U1 B. 1�U2�U3 C. 2�U3�U4 D. 3�U4�U5
C ��������������������ȹ���O����OD��AB��D����OE��AC��E����OF��BC��F���ɵ�O�ǡ�ABC�ڽ�ƽ���ߵĽ��㣬���ݽ�ƽ���ߵ����ʣ����ɵ�OD=OE=OF���̶��ɵã���=AB��BC��CA�������ô𰸣� ����O����OD��AB��D����OE��AC��E����OF��BC��F�� �ߵ�O�ǡ�ABC�ڽ�ƽ���ߵĽ��㣬 ��OD=OE=OF�� �࣬���� ��AB=20��BC...
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
ij��������һ�ֺϽ𱡰壨���Ⱥ��Բ��ƣ���Щ�������״��Ϊ�����Σ��߳�����λ��cm����5��50֮�䣬ÿ�ű���ijɱ��ۣ���λ��Ԫ���������������λ��cm2������������ÿ�ű���ij����ۣ���λ��Ԫ���ɻ����ۺ�������������ɣ�����������=������+�����ۣ����л������뱡��Ĵ�С�أ��ǹ̶�����ģ��������뱡��ı߳�x������������Ӫ�������еõ��˱����е����ݣ���֪����һ�ű߳�Ϊ40cm�ı��壬���������26Ԫ��������=�����۩��ɱ��ۣ�
����ı߳���cm�� | 20 | 30 |
�����ۣ�Ԫ/�ţ� | 50 | 70 |
��1����һ�ű���ij�����y��߳�x֮������ĺ�����ϵʽ��
��2����һ�ű��������p��߳�x֮��ĺ�����ϵʽ��
��3����һ�ű����������34Ԫ���ҳɱ���ͣ���ʱ����ı߳�Ϊ���٣�������ı߳�Ϊ����ʱ����������������������ֵ��
��1��y=2x+10����2��p=��x2+2x+10����3��������ı߳�Ϊ25cmʱ����������������ֵ35Ԫ�� ����������1�����ô���ϵ������һ�κ�������ʽ���ɵó��𰸣� ��2�����ȼ���һ�ű��������ΪpԪ�����ijɱ���Ϊmx2Ԫ�������⣬�ã�p=y-mx2�������ó�m��ֵ�������������ʽ���ɣ� ��3�����ö��κ�������ֵ��ʽ������κ�������ֵ���ɣ� �������� ��1����һ�ű���ı�...

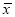 ���䷽��S2���±���ʾ��
���䷽��S2���±���ʾ��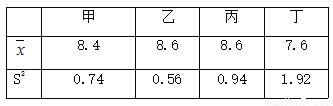
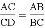 B.
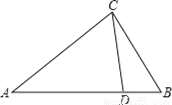
B. 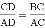 C. AC2=AD•AB D. CD2=AD•BD
C. AC2=AD•AB D. CD2=AD•BD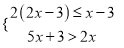 �Ľ⼯�������ϱ�ʾ�����б�ʾ����ȷ���ǣ�������
�Ľ⼯�������ϱ�ʾ�����б�ʾ����ȷ���ǣ�������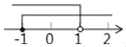 B.
B. 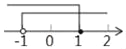 C.
C. 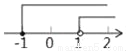 D.
D.