题目内容
2.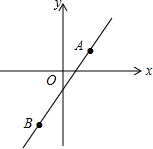 如图,直线AB经过点A(1,1)和点B(-1,-3).
如图,直线AB经过点A(1,1)和点B(-1,-3).(1)求直线AB的解析式;
(2)求直线AB与x轴、y轴围成的三角形的面积.
分析 (1)设直线AB的解析式为y=kx+b,将A(1,1)和点B(-1,-3)代入,利用待定系数法即可求出函数解析式;
(2)求出函数与x轴、y轴的交点坐标,后根据三角形的面积公式即可求解.
解答 解:(1)设直线AB的解析式为y=kx+b,
∵直线AB经过点A(1,1)和点B(-1,-3),
∴$\left\{\begin{array}{l}{k+b=1}\\{-k+b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$.
∴函数的解析式为:y=2x-1;
(2)∵y=2x-1,
∴当x=0,y=-1,当y=0,x=$\frac{1}{2}$,
∴此函数与x轴、y轴围成的三角形的面积为:$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$.
点评 本题考查了待定系数法求一次函数解析式及三角形的面积,难度不大,属于基础题,注意细心运算即可.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
13.下列图形,既是中心对称图形,又是轴对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 正五边形 | D. | 正六边形 |
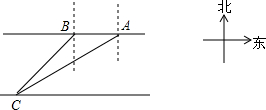 一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点A处观测到河对岸有一点C在A的南偏西59°的方向上,沿河岸向西前行20m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度.(参考数据:tan31°≈$\frac{3}{5}$,sin31°≈$\frac{1}{2}$)
一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点A处观测到河对岸有一点C在A的南偏西59°的方向上,沿河岸向西前行20m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度.(参考数据:tan31°≈$\frac{3}{5}$,sin31°≈$\frac{1}{2}$)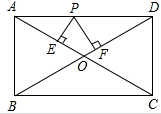 已知矩形ABCD中,对角线交于点O,AB=6cm,BC=8cm.P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值是多少?这个值会不会随着点P的一定(不与A、C重合)而改变呢?请说明理由.
已知矩形ABCD中,对角线交于点O,AB=6cm,BC=8cm.P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值是多少?这个值会不会随着点P的一定(不与A、C重合)而改变呢?请说明理由.