题目内容
1. 如图,在Rt△ABC中,CD是斜边AB上的高线,已知S△ACD:S△CBD=4:9,AC=6,求△ABC的周长和面积.
如图,在Rt△ABC中,CD是斜边AB上的高线,已知S△ACD:S△CBD=4:9,AC=6,求△ABC的周长和面积.
分析 根据CD是斜边AB上的高,利用直角三角形两锐角互余的性质求证∠A=∠BCD,然后即可求证△ACD∽△CBD,根据相似三角形的性质得到BC,根据勾股定理求得AB,即可得到结论.
解答 解:∵CD是斜边AB上的高.
∴∠ADC=∠CDB=90°,
又∵在Rt△ABC中,∠C=90°,
∴∠ACD+∠BCD=90°
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴$\frac{AC}{BC}=\sqrt{\frac{{S}_{△ACD}}{{S}_{△BCD}}}$=$\frac{2}{3}$,
∴BC=9,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{9}^{2}}$=3$\sqrt{13}$,
∴△ABC的周长=AB+AC+BC=15+3$\sqrt{13}$,
S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}×6×9$=27.
点评 此题主要考查相似三角形的判定与性质,勾股定理,三角形的面积和周长的求法,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
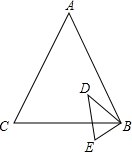 如图,已知在△ABC和△EBD中,$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$.
如图,已知在△ABC和△EBD中,$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$. 如图,AB,CD相交于点O,AC∥BD,已知DB:AC=3:5,△DBO的面积为18cm2,求△CAO的面积.
如图,AB,CD相交于点O,AC∥BD,已知DB:AC=3:5,△DBO的面积为18cm2,求△CAO的面积.